Proof systems for general statements about discrete logarithms

发表于 更新于 分类于

离散对数的一般声明的证明系统

离散对数知识的证明系统是密码学的一个重要基础。我们确定了基本的基础技术，概括了这些技术以证明离散对数之间的线性关系，并提出了一个描述离散对数知识的复杂和一般声明的符号。这个符号直接导致了一种构建高效的知识证明系统的方法。

1 介绍

许多复杂的加密系统，如支付系统（例如见 [1，2，4]）和投票方案 [11]，都是基于离散对数问题的难度。这些系统利用了各种关于离散对数的最小披露证明 [13, 7, 6, 10]。典型的例子是基于 Schnorr 数字签名方案的离散对数知识的有效证明 [18] 和用于证明两个离散对数相等的系统，如在 [8] 中使用。

本文的目标是确定证明离散对数声明的基本技术，对其进行概括，并为指定可使用这些概括技术证明的离散对数声明提供一个正式的符号。特别是，该符号允许定义关于离散对数知识的声明，关于它们之间的（线性）关系，以及关于其原子也是声明的单调的布尔函数。然后，这个符号导致了一种从推测中推导出有效证明系统的方法。

De Santis 等人 [12] 和 Cramer 等人 [10] 已经提出了构建复杂证明系统的类似方法。特别是，给定单个语句的证明系统，他们展示了如何为这些语句上的任何单调布尔公式构造一个证明系统。尽管我们把自己限制在关于离散对数（和表示）的语句上，但我们的方法是对 [12，10] 的概括，因为它还包括证明证人之间关系的可能性（例如离散对数）。例如，使用 [12, 10] 的方法，两个离散对数相等的证明不能从离散对数知识的简单证明中得出。

在第 2 节中，我们简要地描述了离散对数和表示问题，并列出了一些符号。在第 3 节中，我们非正式地介绍了知识的证明，并介绍了一些基于离散对数的证明的例子。在第 4 节中，我们讲述并解释了关于离散对数的具体陈述的符号。然后，我们在第 5 节中表明，给定这样一个规格，如何构建一个有效的证明系统（一个例子可以在第 6 节中找到）。本文在第 7 节结束时讨论了可能的改进和开放的问题。

2 预备工作

让 是一个阶为素数 的有限循环群，让 是 的生成元，对于一些 （注意 的原始性不是一个必要条件，但为了简单起见，在此假设）。一个元素 对基数 的离散对数是唯一的整数 ，即 ，其中 。离散对数也被称为 相对于基数 的索引。关于基数 的 的索引元组是一个 元组 ，对于 ， ，并且 。索引元组 也被称为 相对于 的表示。关于表示问题的进一步讨论见 [1]。

现在让我们用一些将在本文中使用的符号来表示。字符串 和 的连接用 表示。表达式 意味着 根据均匀分布从（有限的）集合 中随机选择。 最后，让 ，表示一个抗碰撞的哈希函数，它将参数的二进制表示法映射为长度为 的二进制字符串（例如 ）。

3 知识证明

非正式地，知识证明允许承诺方说服（证明给）验证方，他知道一个难以解决的问题的解决方案，从而使以下属性成立。

  • 一个诚实的承诺方，知道一个解决方案，可以成功地说服验证方（完整性）。

  • 绝大多数情况下，一个作弊的承诺方不知道任何解决方案，将无法说服验证方（健全性）。

  • 验证方没有得到关于承诺方所知道的解决方案的任何有用信息（关于 "没有得到任何有用信息" 的含义有不同的说法，例如零知识、证人隐藏和最小披露等）。

知识证明在文献 [13] 中被正式引入并命名，但如果系统不符合文献 [13] 的强要求，我们也将称之为知识证明。已经证明，知识证明存在于一大类问题中 [14, 3]。然而，只有一些数论问题，如 RSA 反转和计算离散对数，才发现了有效的证明 [15, 7, 6, 18]。

特别是，对离散对数和表示法的知识证明是许多加密系统的重要组成部分，从简单的身份识别和签名方案到复杂的电子投票和数字支付系统。在第一个例子中，我们将介绍一个关于离散对数知识的简单证明。

例 1：为了证明 的离散对数到基数 的知识，承诺方计算：

  1. ，其中

其中值 称为承诺，值 称为挑战，值 称为回应。由此产生的证明是一对 ，可以通过首先重建承诺 ，然后（由每个人）检查等式 是否成立来验证。这个知识证明基本上是消息 的 Schnorr 签名 [18]。

让我们简单地讨论一下例 1 的证明系统的特性。首先，我们可以很容易地看到，一个诚实的承诺方总是能够成功地构建一个有效的证明，因为： 因此， 。第二，假设一个不知道 的作弊承诺方能够计算出这样的证明。由于散列函数很难被反转，我们可以假设在计算 之前，值 被固定。似乎也有必要在固定值 时，承诺方准备为许多其他可能的挑战计算一个证明（否则成功的概率就太小了）。但这意味着作弊承诺方也可以计算 在基数 和 上的不同表示，这意味着知道 ，即 在基数 上的离散对数，而这与作弊承诺方不知道 的假设相矛盾。最后，在假设 是一个真正的随机函数的情况下，可以证明从这种证明中提取离散对数的难度与计算离散对数一样。如果协议是交互式执行的，即挑战是由验证方从一个 “可能挑战的小的集合” 中选择的，它可以被证明是零知识的（这意味着验证方可以模拟协议中获得的所有信息）。

基于这种对离散对数知识的证明，已经提出了其他几个系统。一个是两个离散对数相等的证明（如在 [9] 中用于一个签名方案）。更一般地说，人们可以证明两个离散对数满足一个线性方程。

例 2：为了证明 和 对基数 和 的离散对数 和 分别满足线性方程 ，承诺方计算：

  1. ， ，其中 ，即
  3. 和

由此产生的证明是 ，可以通过首先重构承诺来进行验证： 然后检查以下等式是否成立： 即： 换句话说，承诺方使验证方相信他：

  • 知道 和 分别到基数 和 的离散对数 和

  • 并且这些对数满足线性方程

乍一看，这像是一种新型的证明系统，即用于证明知识的属性。然而，这些类型的证明可以很容易地使用知识证明的概念进行建模。

下一个例子说明了不同的证明是如何结合的。给出两个问题 和 以及相应的证明解决方案知识的系统，构建一个证明 和 的解决方案知识的系统是很简单的（两个证明系统简单地平行执行）。证明对问题 或问题 的解决方案的了解是比较困难的，因为验证方必须不知道承诺方知道哪个解决方案。一个非常有趣的方法是由 Cramer 等人 [10] 和 De Santis 等人 [12] 独立提出的，用于解决这个问题。让我们在例 3 中演示这个方法。

例 3：为了证明 到基数 的离散对数或 到基数 的离散对数的知识，承诺方计算（假设承诺方只知道 ）：

  1. 和 ，其中
  3. 和
  4. 和

由此产生的证明 可以通过重构承诺来验证： 并检查等式是否成立： 即： 这样做的原因是，承诺方被 “允许伪造” 两个证明中的一个，因为他可以在计算承诺之前选择相应的挑战；另一个挑战则由哈希函数决定。然而，验证方不能决定选择哪一个挑战，因此不能获得关于承诺方知道哪些离散对数的信息。

4 知识规范集

在上一节中，我们介绍了证明有关离散对数和表示法知识的基本原则。这些基本证明现在可以结合起来，以证明更复杂问题的解决方案的知识。我们给出了一个正式的符号来指定一方想要证明的知识。从这个规范中可以得出一个有效的证明系统。在描述这个规格化之前，我们需要给出以下符号。

定义 4.1 组元的串联：

让 和 分别为 和 元组。 和 的连接表示为 ，为元组 。

定义 4.2 修改的笛卡尔积：

让 和 是组元的集合。 和 的修改的笛卡尔积表示为 ，是组元 的集合。

使用这个符号，我们可以得出一个值集（这是底层 NP 语言的见证），知识的证明包括证明这个集合中至少一个元素的知识。我们称这样的集合为知识规范集，其表示法为知识规范。正如介绍中提到的，我们把自己限制在指定有关离散对数和表示法的知识的集合上。

定义 4.3 知识规范集：

假设 是一个阶为素数 的有限群，那么群 的知识规范集表示如下：

  • 对于任何群组元素 和 ，集合 是一个知识规范集。
  • 对于任何 的群组元素 和 ，集合 是一个知识规范集。
  • 对于任何 的值 和 ，集合 是一个知识规范集。
  • 对于知识规范集 和 来说，集合 ， 和 依然是是一个知识规范集。

备注：集合 只包含一个元素，由于离散对数问题，对于给定的 和 ，很难计算这个元素。集合 可以包含一个以上的元素。然而，如果以随机的方式选择基数，就很难计算出已知表示之外的任何其他表示。请注意， 只是 的一个特例，其 。此外，证明一个集合 的一个元素的知识是很困难的，因为很容易计算出方程 的解。然而，这样的集合在与其他使用 运算符的语句相结合时是有意义的，以表达几个离散对数或表示法之间的线性关系。

现在让我们简单地讨论一下知识规范集的几个例子。首先，证明集合 的一个元素的知识相当于证明 对基数 的离散对数的知识，而集合 对应于 对基数 的表示的知识证明。

此外，例 2 中的证明的知识规范集可以用下面的方式表示。它显示了线性方程如何被用于知识规范： 集合 正好包含一对由 和 分别对基数 和 的离散对数组成的集合。当且仅当这两个对数满足线性方程时， 和 的交集是不空的。因此，通过证明对集合 的一个元素的知识，承诺方间接地证明了 是非空的，因此这两个离散对数具有所需的属性。

利用集合的联合，我们还可以指定更多的一般性声明，例如，证明两个离散对数是已知的，并且至少满足两个线性方程中的一个： 让我们对知识规范集的相交做一个最后的备注。如果一个人与包含不同势的组元的集合相交，比如说： 很明显，所产生的集合是空的，因此不可能有证明。因此，我们将在后文中假设，在知识规范中消除这种表达。

5 证明系统的构建

在这一节中，我们将展示如何构建一个证明系统，以证明任意知识规范集的一个元素的知识。

转化和树状表征

让 是一个知识规范。通过对 和它的子表达式应用变换：

我们可以找到 的一个表示，形式为 ，其中，规范 不包含形式为 的子表达式。从现在开始，我们将把这些 看作二叉树，其叶子是类型为 、 或 的表达式，其内部节点是类型为 或者 的表达式（见图 1 的例子）。节点的标记如下：

  • 树 的根被标记为
  • 标记为 的节点的左孩子被标记为
  • 标记为 的节点的右孩子被标记为
Figure 1

图 1：集合 表示为两棵二叉树的森林（也见附录中例 4）。节点的标签印在每个节点的左边。

现在，树 中的每个节点 都被分配了一个 二元组，其中 是一个变量的元组， 是一组在 中的变量和特殊变量 中的有限域 的方程。这些二元组被递归地表示为：

  • 如果 是一个 类型的叶子，则 ， 。
  • 如果 是 类型的叶子，则 ， 。
  • 如果 是 类型的叶子，则 ， 。请注意，树 中所有 类型的节点都使用同一个变量 。
  • 如果 是一个类型为 的内部节点，则 ，
  • 如果 是一个类型为 的内部节点，则 ，

在最后一个方程式中， 表示元组 中的第 个变量。最后，让 ， ， 。

和 是一串变量， 是 和 中的变量的线性方程组（模 ）。在下文中，我们将使用 的符号，意思是在 中， 的变量被相应的值所取代。

构建 F 的证明

一个 (诚实的) 承诺方知道一个元素 ，它必须包含在至少一个集合 中。因此，存在一个索引 ，使得 。注意 是 的元素的一个元组。然后，知识的证明被构建如下：

  1. 承诺

    1. 计算 ，其中 ，其他 对于 。

    2. 分配给 一个随机元组，满足 。

    3. 以下列方式给森林 中的每个节点 分配一个承诺 ：

      • 如果 是树 中 类型的叶子，那么：

      • 如果 是树 中 类型的叶子，那么：

      • 如果 是一个 类型的叶子，那么 是空元组 。

      • 如果 是一个类型为 或 的内部节点，那么：

    然后，承诺 被计算为：

  2. 挑战

    挑战 的计算方法如下：

  3. 响应

    给定 ，承诺方可以构建一个满足以下条件的元组 （ 的组成部分的标记方式与 的组成部分的标记方式相同）：

    • 如果叶子 不在树 上，对于所有索引 ， 。
    • 如果 是树 中的 或 类型的叶子，那么子元组 是由叶子的类型表示的集合中的一个元素。
    • 满足等式 （其中 是 的子元组，对应于 的子元组 )

    对于所有的叶子 和所有的指数 ，响应 ，然后用以下方式表示：

知识的证明是 对。

验证一个证明

对一个证明 的验证包括以下两个步骤：

  1. 通过给森林 中的每个节点 分配一个元组 ，以如下方式重建承诺：

    • 如果 是树 中 类型的叶子，那么：

    • 如果 是树 中 类型的叶子，那么：

    • 如果 是一个 类型的叶子，那么 是空元组 。

    • 如果 是一个类型为 或 的内部节点，那么：

    重构后的承诺 为：

  2. 通过以下方式验证挑战和回应：

    • 验证
    • 验证 能满足

6 例子

下面的例子应该可以说明第 5 节中提出的方法。

例 4：假设承诺方知道 , 和 ，从而知道 ， 和 ，并想证明 到基数 的离散对数和 到基数 和 的表示的知识。此外，他想证明 或者 成立（当然不需要给出 , 和 的进一步信息）。

这个证明的知识规范是： 为了构建证明系统，该规范必须首先被转换为树状表示，这可以通过应用转换 III 来实现，即 ： 这个森林展现在图 1 中。

接下来，承诺方必须为每个节点建立变量列表和方程组。这里我们只对树 做了这个工作，树 的列表和方程组看起来差不多：

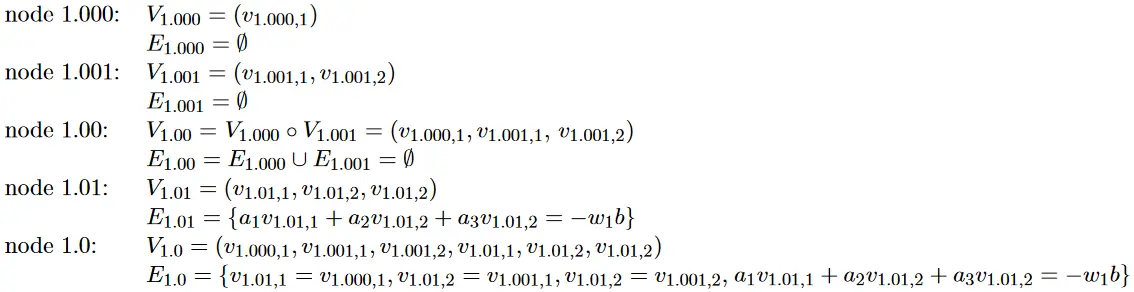
image-20221207151703453

其中， 最后， 和 的集合被合并，承诺方得到 ，它是 上的下列方程集合： 并且在指定了 和 之后，承诺方就能够构建证明。他选择 为 ，其中 ，以及一个满足方程 的随机元组 。这可以通过在 中随机选择 来实现，从而使以下等式成立： 并指定 。

现在可以计算出各节点的承诺：

image-20221205163152150

因为 ，承诺方可以计算出挑战值： 为了计算响应 ，承诺方建立了 的列表（注意 ），并计算 的组成部分 （所有方程均为模 ，组成部分按正确顺序排列）：

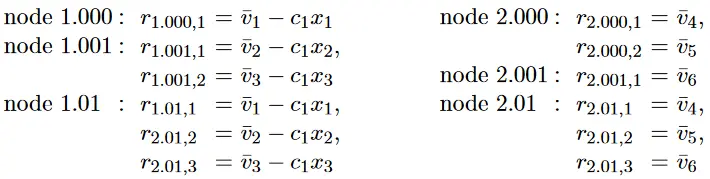
image-20221205163443444

由此产生的证明是 对。

现在让我们看看验证方如何着手检查证明的有效性。第一步，验证方必须通过给 和 中的每个节点分配一个元组 来重建承诺：

image-20221205163644123

并得到 。然后验证方检查挑战和 的方程（同样，所有方程都是模 的）。

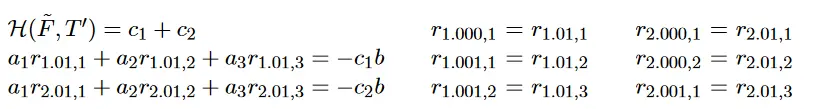
image-20221205163825467

可以很容易地看出，如果按照上述方法构建证明，这些方程是成立的。

7 扩展和开放性问题

在这份报告中，我们展示了如何构建复杂的知识证明。为了使符号和推导证明的方法尽可能的简单，我们省略了几个可能的扩展和优化措施。

其中一些扩展和改进是非常明显的。例如，承诺方可以不返回必须满足 中的方程的整个元组 ，而只发送 中足够多的成分，以便用 中的线性方程计算其他成分。在例 4 中，它成功地返回了 ， , 和 的值；然后 的所有其他八个成分可以很容易地从线性方程中计算出来。

另一个简单的扩展是将不同组中的离散对数知识的证明结合起来，甚至是将不同问题的证明结合起来。然而，我们应该注意不要让不同类型的集合相交，因为这可能会导致对证明的误解。

最后，使用来自 [17，16] 的技术，证明也可以盲目地发出，这意味着承诺方帮助接受者获得一个有效的知识证明，而不需要获得有关信息。这种 "盲目发行" 证明的一个重要应用是匿名保护数字支付系统（例如，见 [1，2，5]）。

一个有趣的开放性问题是设计与非线性方程相结合的有效知识证明，例如证明一个离散对数等于另一个离散对数的三次方（有一些非线性关系可以被有效地证明，例如证明一个离散对数是另一个对数的平方或逆，但似乎很难推广这些方法）。

鸣谢

第一作者得到了瑞士联邦技术与创新委员会（KTI）和瑞士联合银行的支持。

参考文献

  1. S. Brands. An eficient off-line electronic cash system based on the representation problem. Technical Report CS-R9323, CWI, Apr. 1993.

  2. S. Brands. Untraceable off-line cash in wallets with observers. manuscript, CWI, 1993.

  3. G. Brassard, C. Crepeau, and M. Yung. Everything in NP can be argued in perfect zero-knowledge in a bounded number of rounds. In G. Ausiello, M. Dezani-Ciancaglini, andS.R.D.Rocca,editors,Proceedings of 16th ICALP, volume 372 of Lecture Notes in Computer Science, pages 123-136. Springer-Verlag, 1989.

  4. J. Camenisch, U. Maurer, and M. Stadler. Digital payment systems with passive anonymity-revoking trustees. In E. Bertino, H. Kurth, G. Martella, and E. Montolivo, editors, Computer Security | ESORICS 96, volume 1146 of Lecture Notes in Computer Science, pages 33-43. Springer Verlag, 1996.

  5. J. Camenisch, J.-M. Piveteau, and M. Stadler. An eficient fair payment system. In 3rd ACM Conference on Computer and Communicatons Security, pages 88-94, New Delhi, Mar. 1996. Association for Computing Machinery.

  6. D. Chaum, J.-H. Evertse, and J. van de Graaf. An improved protocol for demonstrating possession of discrete logarithms and some generalizations. In D. Chaum and W. L. Price, editors, Advances in cryptology | EUROCRYPT '87, volume 304 of Lecture Notes in Computer Science, pages 127-141. Springer-Verlag, 1988.

  7. D. Chaum, J.-H. Evertse, J. van de Graaf, and R. Peralta. Demonstrating possession of a discrete logarithm without revealing it. In A. M. Odlyzko, editor, Advances in Cryptology | CRYPTO '86, volume 263 of Lecture Notes in Computer Science, pages 200-212. Springer-Verlag, 1987.

  8. D. Chaum and T. Pedersen. Transferred cash grows in size. In R. A. Rueppel, editor, Advances in Cryptology | EUROCRYPT '92, volume 658 of Lecture Notes in Computer Science, pages 390-407. Springer-Verlag, 1993.

  9. D. Chaum and T. P. Pedersen. Wallet databases with observers. In E. F. Brickell, editor, Advances in Cryptology | CRYPTO '92, volume 740 of Lecture Notes in Computer Science, pages 89-105. Springer-Verlag, 1993.

  10. R. Cramer, I. Damgard, and B. Schoenmakers. Proofs of partial knowledge and simplified design of witness hiding protocols. In Y. G. Desmedt, editor, Advances in Cryptology | CRYPTO '94, volume 839 of Lecture Notes in Computer Science, pages 174-187. Springer Verlag, 1994.

  11. R. Cramer, M. Franklin, B. Schoenmakers, and M. Yung. Multi-authority secret-ballot elections with linear work. In U. Maurer, editor, Advances in Cryptology | EUROCRYPT '96, volume 1070 of Lecture Notes in Computer Science, pages 72-83. Springer Verlag, 1996.

  12. A. De Santis, G. Di Crescenzo, G. Persiano, and M. Yung. On monotone formula closure of SZK. In 35th Annual Symposium on Foundations of Computer Science, pages 454-465, Santa Fe, New Mexico, 20-22 Nov. 1994. IEEE.

  13. U. Feige, A. Fiat, and A. Shamir. Zero-knowledge proofs of identity. Journal of Cryptology, 1:77-94, 1988.

  14. O. Goldreich, S. Micali, and A. Wigderson. How to prove all NP statements in zeroknowledge and a methodology of cryptographic protocol design. In A. M. Odlyzko, editor, Advances in Cryptology | CRYPTO '86, volume 263 of Lecture Notes in Computer Science, pages 171-185. Springer-Verlag, 1987.

  15. L. C. Guillou and J.-J. Quisquater. A practical zero-knowledge protocol fitted to security microprocessor minimizing both transmission and memory. In C. G. G ̈ unther, editor, Advances in Cryptology | EUROCRYPT '88, volume 330 of Lecture Notes in Computer Science, pages 123-128. Springer Verlag, 1988.

  16. T. Okamoto. Provable secure and practical identification schemes and corresponding signature schemes. In E. F. Brickell, editor, Advances in Cryptology | CRYPTO '92,volume 740 of Lecture Notes in Computer Science, pages 31-53. Springer-Verlag, 1993.

  17. T. Okamoto and K. Ohta. Disposable zero-knowledge authentications and their applications to untraceable electronic cash. In G. Brassard, editor, Advances in Cryptology | CRYPTO '89, volume 435 of Lecture Notes in Computer Science, pages 481-496. SpringerVerlag, 1990.

  18. C. P. Schnorr. Eficient signature generation for smart cards. Journal of Cryptology, 4(3):239-252, 1991.