Fast Private Set Intersection from Homomorphic Encryption

发表于 更新于 分类于

基于同态加密的快速隐私保护集合求交

隐私保护集合求交（PSI）是一种加密技术，它允许双方在不透露任何东西的情况下计算他们的集的交集，除了交集。我们使用完全同态加密来构建一个快速的 PSI 协议，其通信开销很小，当两个集合中的一个比另一个小得多时，该协议特别好用，并且对半诚实的对手是安全的。

计算效率最高的 PSI 协议是使用哈希函数和不经意传输等工具构建的，但这些方法的一个潜在限制是通信复杂度，它与较大集合的大小呈线性扩展。当在一个持有小集合的受限设备（手机）和一个大型服务提供商（如 WhatsApp）之间执行 PSI 时，这是一个特别值得关注的问题，例如在私人联系人发现应用中。

我们的协议的通信复杂度与小集合的大小成线性关系，而与大集合成对数关系。更确切地说，如果集合的大小是 ，我们实现的通信开销是 。我们的运行时间优化基准显示，将 5000 个 32 位字符串与 1600 万个 32 位字符串相交，需要 36 秒的在线计算，71 秒的非交互式（独立于接收器）预处理，以及仅 12.5MB 的往返通信。与之前的工作相比，这大约减少了 38-115 倍的通信量，而计算开销的差别很小。

1 介绍

1.1 隐私保护集合求交

隐私保护集合求交（PSI）指的是这样一种情况：双方各自持有一个私有项目集，并希望在不透露任何信息的情况下学习他们的集合的交集，除了交集本身。在过去的几年里，由于一长串的出版物，例如 [9, 18, 37, 39, 46, 48-50, 53]，PSI 已经成为真正实用于各种应用。最有效的协议是由 Pinkas 等人 [50] 和 Kolesnikov 等人 [37] 提出。虽然这些协议非常快，但它们的通信复杂度在两个集合的大小上是线性的。当一个集合明显小于另一个集合时，与非私有解决方案相比，通信开销变得相当大，后者的通信量与较小集合的大小呈线性关系。

1.2 全同态加密

全同态加密是一个强大的加密原语，它允许算术电路直接在加密的数据上进行评估，而不是先解密数据。尽管其基本思想很古老 [54]，但在 2009 年才由 Craig Gentry [25] 给出第一个构造。虽然早期的全同态加密方案是不切实际的，但在短短几年内，研究人员设法构建了更有效的方案（例如 [8, 12, 13, 21, 28, 41]），使实际应用接近于现实 [26, 29, 45]。

乍一看，使用完全同态加密来实现 PSI 中的低通信成本似乎很容易。拥有较小集合的一方将其加密的集合发送给另一方，后者以同态方式评估交集电路，并将加密的结果发回给第一方进行解密。总的通信量只有 然而，对上述想法的天真实施将导致一个非常低效的解决方案。原因是，对于所有已知的完全同态加密方案，计算成本不仅随着输入的大小（在这种情况下，两个集合大小的总和）而增长，而且还随着电路的深度而迅速增长。 因此，我们的主要挑战是提出各种优化方案，使该方案切实可行，甚至在许多情况下比最先进的协议更快。简而言之，我们将表明有可能构建一个快速的基于全同态加密的 PSI 协议，而且通信开销很低。

1.3 相关工作

Meadows [44] 提出了最早的安全 PSI 协议之一，后来 Huberman、Franklin 和 Hogg 在 [34] 中对其进行了全面描述。这种方法是基于公钥密码学，并利用了 Diffie-Hellman 密钥交换的乘法同构特性。虽然这些方案具有相对较好的通信成本，但由于需要对两个集合中的每一项进行多次的模块化指数化，当集合大小变得很大时，运行时间可能会很漫长。

自 [34] 以来，人们考虑了其他一些范式。Freedman 等人 [23] 提出了一个基于不经意多项式评估的协议。这种方法利用了部分同态加密，后来在 [15, 31, 32] 中被扩展到恶意设置。另一种方法是由 Hazay 等人 [30] 提出的，并基于所谓的不经意式 PRF。

最近，人们发明了基于不经意传输（OT）的更有前途的方法 [35, 46]。当时，到目前为止，最有效的方案是由 Pinkas 等人提出的 [49]，后来在 [37, 46, 50] 中得到改进。我们将用发送方和接收方来表示参与 PSI 协议的两方，并坚持认为在协议执行后，接收方会了解到集合的交集，而发送方则不会了解到任何信息。基于 OT 的协议的高层次想法是，接收方与发送方进行许多 OT，并为其集合中的每个项目忘我地学习随机编码，而不透露哪些值被编码。然后，发送方可以对其项目进行本地编码，并将其发送给接收方，接收方在编码上计算出明文交集。由于编码是随机的，它们不会透露任何超出交集的信息。这种方法的一个固有属性是，由于需要对所有的编码进行编码和发送，通信在两个集合的大小上都是线性的。我们采取的方法是类似的，只是我们使用完全同态加密来代替不经意传输。

然而，另一种基于 OT 的方法是由 Dong 等人引入的 [18]，它建立在一个被称为布鲁姆过滤器的数据结构上。这种数据结构允许通过在一个长的位阵列中设置特定的位来进行有效的成员测试。重要的是，两个布隆过滤器的位和本身就是两个原始集合的交集的有效布隆过滤器。通过对这一想法进行一些修改，就可以构建一个安全的协议，允许其中一方通过使用 OT 来学习两个布隆过滤器的位 - 明智和。这种方法比 Pinkas 等人 [49] 介绍的方法需要更大的通信量，并且导致性能下降。

通常引用的 PSI 的解决方案是使用通用的安全多方计算协议来计算交集。Huang 等人 [33] 是第一个使用乱码电路实现这种协议的人，后来 [49] 对此进行了改进，并提供了一个实现。他们表明，与基于 OT 的方法相比，乱码电路方法需要明显更多的通信。对于实际方法的更完整的调查，我们提请读者参考 [50]。

Kamara 等人也提出了一个非常有效的服务器辅助协议 [36]。在这种情况下，假设存在一个非拥挤的服务器。其基本思想是，在双方之间取样一个随机函数，将其应用于各自集合中的元素。然后，这些编码被发送到服务器，由其报告相交情况。虽然在概念上很简单，而且非常有效，但对这种服务器的依赖是不可取的。此外，通信的复杂性在两个集合的大小上是线性的。

在上述所有协议中，都假定在协议开始时，集合的大小（或上界）是公开的。Ateniese 等人 [6] 介绍了一个基于 RSA 累加器的协议 [7]，它通过隐藏接收者的集合大小来放松这一假设。这个协议的工作原理是让接收方为其集合构建并发送一个 RSA 累加器。然后，发送方可以为其每个项目构建一个响应，这使得接收方可以测试它们是否包含在 RSA 累加器中。RSA 累加器的一个重要属性是它的大小很小，而且与接收方的集合大小无关。因此，当接收方有一个比发送方大得多的集合时，这个协议是最有趣的。在后续工作中，Bradley 等人 [10] 将该协议扩展到对累加器中的项目数量施加一个上限，从而防止接收方的所谓 "全域攻击"。

1.4 贡献和路线图

正如我们的讨论所示，所有先前的 PSI 协议都要求双方在网络上编码并发送与他们整个集合成比例的数据。然而，琐碎的不安全的解决方案只要求发送较小的集合。我们通过构建第一个安全实用的、具有低通信开销的、基于平坦的全同态加密方案的 PSI 协议来解决这一差距。

我们的基本协议需要在较小的集合中进行线性通信，实现与天真的解决方案相同的最佳通信。然后，我们结合一系列的优化，以显著减少通信规模、计算成本和同态电路的深度，同时只增加通信的对数开销。总而言之，我们

  • 提出一个基于全同态加密的基本 PSI 协议。
  • 结合各种优化措施，大大降低计算和通信成本。
  • 使用微调的全同态加密参数进行同态计算，以避免昂贵的引导操作 [25, 26]，并获得良好的性能。
  • 用 C++ 开发一个原型实现，并证明比以前最先进的协议减少 38-115 倍的通信量。

在第 2 节中，我们回顾了我们用来建立协议的设置和工具：PSI 设置和它的安全定义，以及关于（平坦的）完全同态加密的初步知识。在第 3 节，我们提出了我们的基本草根 PSI 协议。然后，在第 4 节中，我们应用优化方法来大大改善草根协议，并使其实用。第 5 节介绍了优化协议的形式描述，以及安全证明。在第 6 节中，我们对我们的实现进行了性能分析，并将我们的性能结果与 [50] 和 [37] 进行比较。

2 初步了解

2.1 符号

在本文中，我们将使用符号 来表示 的集合。计算和统计安全参数将分别用 、 来表示。其他参数包括：

  • 是发送方和接收方的集合，每个集合的大小为 。
  • 表示哈希表的大小， 表示要插入哈希表的项目数。
  • 表示第 2.3 节中描述的加密参数。
  • 表示第 4.2 节中用于布谷鸟散列的哈希函数的数量。
  • 表示第 4.2 节中描述的简单散列方案的桶大小。
  • 表示第 4.3.1 节所述的窗口化参数。
  • 表示第 4.3.2 节中描述的分区参数。

2.2 隐私保护集合求交

我们使用标准的符号，把参与 PSI 的两方称为发送方和接收方。发送方持有一个大小为 的集合 ，而接收方持有一个大小为 的集合 。两个集合都由 位字符串组成。我们总是假设集合的大小 和 是公开的。理想的 PSI 功能计算交集，不向发送方输出任何信息，并向接收方输出 。我们从完全同态加密中构建了一个新的 PSI 协议，并证明它在半诚实的安全模型中是安全的，其中双方都正确地遵循协议，但可能试图从他们对协议执行的看法中尽可能多地学习。 当发送方的集合比接收方的集合大得多时，我们的协议就特别强大。因此，我们在整个论文中假设 ，尽管该协议对任意的集合大小都适用，没有任何变化。更确切地说，我们实现了的通信复杂性。此外，我们只要求发送方执行与较大的集合大小 成线性的工作。直观地说，接收者加密并将其集合发送给发送者，发送者通过评估一个适当的比较电路来计算同态加密数据的交集。然后，输出被压缩到更小的尺寸，使用同态乘法，并送回给接收方进行解密。我们注意到，接收方在协议中只进行了相对较少的计算，即对数据的加密和解密与它的集合大小 线性相关。当接收器的计算能力有限时，这一点特别有用，例如，当接收器是一个移动设备时。

2.2.1 发现隐私关联

我们的 PSI 协议的一个特别有趣的应用是私人联系人发现。在这种情况下，一个服务提供商，例如 WhatsApp，有一组几百万的用户。这些用户中的每个人都拥有自己的联系人集，并希望了解其中哪些人也使用该服务。这个问题的不安全解决方案是让用户把他们的联系人集合发送给服务提供商，然后由服务提供商代表用户进行交集。虽然这保护了服务提供者的隐私，但却将用户的私人联系人泄露给服务提供者。 虽然 PSI 为这个问题提供了一个自然的解决方案，但将现有的协议应用到这个环境中的一个潜在问题是，双方的通信和计算复杂性在更大的集合中是线性的。因此，一个可能只有几百个联系人的用户必须接收和处理与该服务的用户数量成线性关系的数据，这导致了对受限硬件（如手机）的次优协议。这个问题最初是由 Open Whisper Systems 的 Moxie Marlinspike 在一篇文章中提出的 -- 该公司开发了流行的安全信息应用 Signal-- 当时他们正试图部署 PSI 用于联系人发现 [43]。我们的 PSI 协议通过允许受限设备处理和接收仅与它们的集合大小成线性关系，而仅与服务提供商的集合大小成对数关系的数据来解决这个问题。此外，计算的主要部分可以由服务提供者在处理能力相对便宜的大型数据中心进行，而用户只进行轻微的计算。

2.3 分级的全同态加密

全同态加密方案是允许算术电路直接在密码文上进行评估的加密方案，理想情况下可以实现强大的应用，如隐私数据的外包计算 [25, 54]。为了提高性能，加密参数通常被选择为只支持一定深度的电路（分级全同态加密），我们在实现中使用了这一点。

本文介绍的许多技术和算法与正在使用的确切的完全同态加密方案无关，但为了简单起见，我们将其限制在基于环容错学习问题 (ring learning with errors, RLWE) 的密码系统，使用整数的 2 次方环 [42]。在这种密码系统中，明文空间是 ，而密文空间是 ，其中 是 2 的幂， 且是整数。习惯上表示 ，因此明文和密文空间分别成为 ，。我们假设完全同态加密方案有这种类型的明文和密文空间，而符号 将总是指这些参数。例如，Brakerski-Gentry-Vaikuntanathan（BGV）[12] 和 Fan-Vercauteren（FV）[21] 方案具有这种结构。

一个分级的全同态加密方案可以由以下一组随机算法来描述。

  • ：给定一个安全参数 ，输出一组加密参数 。
  • ：输出一个密匙 和一个公钥 。可以选择输出一个或多个计算密钥 。
  • ：给定信息 ，输出密文 。
  • ：给定密文 ，输出信息 。
  • ：给定一个有 条输入线的算术电路 ，以及输入，其中 ，输出一个密文 ，使得 。我们还要求 的输出大小不超过 的多项式，与 是什么无关（紧凑性）（见例如 [4]）。

我们说，如果一个完全同态的加密方案是 IND-CPA 安全的，并且是弱循环安全的，这意味着即使对手得到了秘密密钥的比特的加密，该方案仍然是安全的。如果任何固定的同态评估的输出分布与明文输出的新加密分布不可区分，那么一个完全同态的加密方案就实现了电路隐私。通过这种方式，可以有效地隐藏在加密数据上评估的电路。我们请读者参考 [4，12，19] 以了解更多细节。

3 基本协议

我们在图 1 中把我们的基本协议描述为一个稻草人协议。接收方对其每个项目 进行加密，并将其发送给发送方。对于每一个 ，发送方然后以同态方式评估 与发送方所有项目 的差值乘积，通过与一个统一随机的非零明文相乘来随机化该乘积，并将结果发回给接收方。当 在发送方的集合中时，结果正好解密为零，否则解密为一个均匀随机的非零明文，不向接收方透露任何关于发送方集合的信息。

image-20220524143225546
图 1：基本的 PSI 协议

  • 输入：接收者输入大小为 的集合 ；发送者输入大小为 的集合 。两个集合都由长度为 的比特串组成。 是公开的。

  • 输出：接收者得到集合 和集合 的交集 ；发送者什么也没能得到。

  • 步骤：

    1. 设置：发送方和接收方共同商定一个全同态加密方案。接收方生成一对公私钥，并保存私钥。

    2. 加密：接收方对其集合 中的每个元素 进行加密，并将密文 发送给发送方。

    3. 计算交集：发送者对于每个 执行：

      1. 采样一个随机的非零明文元素 。

      2. 同态计算：

      发送方将密文 返回给接收方。

    4. 回复提取：接收者对密文 进行解密并输出：

更准确地说，我们从现在开始假设我们的 FHE 方案中的明文模数 是一个素数，大到足以将 位字符串编码为 的元素。我们还暂时将明文空间限制为常数多项式的子环（这一限制将在第 4.1 节中取消），并假设明文只是 的元素。回顾一下，集合 和 的大小，以及项目的（共同）比特长度 ，都是公共信息。

关于基本协议的安全性和正确性，我们有以下非正式定理。

定理 3.1（非正式）：图 1 中描述的协议在半诚实的安全模型中安全而正确地计算了 和 的私有集交集，前提是全同态的加密方案是 IND-CPA 安全的，并且实现了电路隐私。

证明：接收者的安全是直接的：接收者发送一个密码文数组，在发送者看来是伪随机的，因为全同态加密方案是 INDCPA 安全的。对于发送方的安全，我们注意到，接收方的观点由密码文数组组成。从电路隐私中可以看出，接收方只知道这些密码文本的解密，而没有其他。

对于一个固定的指数 ，我们有： 准确地说，当 时，它是零，否则就是 中一个均匀的随机元素，因为 是一个场。因此，除了 的交集之外，接收者没有学到任何额外的信息。

这种基本协议效率极低：它要求发送方进行 同态乘法和加法，而且电路深度很高，将 FHE 参数大小推到巨大。此外，发送方和接收方需要通信 的 FHE 密文，即使对于最先进的全同态加密方案来说，这也是令人望而却步的。因此，当该协议与下一节所述的增强功能相结合时，变得非常高效，这一点非常令人惊讶。

4 优化

4.1 并行

我们提高性能的第一步是通过使用并行处理，这是完全同态加密中众所周知的强大技术，可以对密码文进行 SIMD（单指令、多数据）操作。我们在这里做一个简单的解释，并请读者参考 [11, 26, 29, 38, 55] 以了解更多细节和应用实例。

对于明文模数 的适当选择，有一个从明文空间 到 的环形同构。例如，一个常数多项式 对应于向量 。此外，这种同构将多项式的加法和乘法转化为 个场 中每个场的系数加法和乘法。为了简化论述，我们交替使用明文的多项式和矢量符号，省略了从一种表示法到另一种表示法的转换。

我们可以应用批处理来减少基本协议的计算和通信成本，具体如下。接收方将其项目分组为长度为 的向量，对其进行加密，并向发送方发送 密文。在看到每个密文 时，发送者对 的均匀随机非零元素的向量 进行采样，同态计算 ，并将其送回给接收者。请注意，这些修改并不影响正确性或安全性，因为完全相同的证明可以适用于每一个矢量系数。

批量技术允许发送方同时对接收方的 个项目进行操作，从而使计算和通信都有 倍的改善。由于在典型的情况下， 的大小为几千，这导致了对基本协议的重大改进。

4.2 哈希

即使有了第 4.1 节的并行处理技术，发送方仍然需要将其每个集合元素编码为单独的明文，并单独与接收方的项目进行比较。相反，如果发送方也能利用批处理的优势，那就更好了。我们将通过使用散列技术来实现这一点。具体来说，我们将批处理与布谷鸟散列和基于置换的散列结合起来使用，这些技术已经在 PSI 的背景下被详细开发和探讨过，例如 [48, 49]。

在进入布谷鸟散列和基于置换的散列的技术问题之前，我们先从高层次解释为什么散列在我们的环境中是有益的。假设两方使用某种商定的确定性散列函数将其集合中的项目散列到两个散列表中。现在他们只需要对每个仓进行一次 PSI，因为不同仓中的项目必然不同。

有一点很重要，那就是所有的桶都必须被填充到一个固定的尺寸以保持安全。请注意，填充前的桶会有不均匀的负载，特定的桶的负载（映射到桶中的物品数量）可以揭示出交叉点以外的额外信息。为了克服这个问题，我们需要用假的物品填充每个仓，直到预先确定的最大尺寸。

刚才描述的简单散列技术大大降低了我们协议的复杂性。众所周知，将 个项目散列到尺寸 的哈希表中，其最大负载很可能是 。例如，在双方都有 个项目的情况下，基本协议的总体复杂度降低到 ，其中 因素来自于在单个桶上执行基本 PSI 协议。接下来，我们将通过更好的散列技术进一步降低复杂性。

4.2.1 布谷鸟哈希

布谷鸟散列 [16, 22, 47] 是一种通过使用 的散列函数 来建立密集散列表的方法。为了插入一个项目 ，我们从 中随机选择一个索引 ，并在表中的 位置插入元组 ，。如果这个位置已经被一个元组 ， 占据，我们用 ， 替换 ，，从 中随机选择一个 ，并递归地将 ， 重新插入到表中。对于 和相当小的 ，布谷鸟散列以非常高的概率成功，即递归重新插入过程总是在达到预先确定的递归深度的上限之前成功。我们将在第 4.2.3 节讨论布谷鸟散列的成功概率。

为了将布谷鸟散列应用于我们的 PSI 协议，我们必须确保逐个桶地比较将总是产生正确的交集。这是通过让接收方用 个桶进行布谷鸟散列来实现的。发送方必须使用所有 个哈希函数（简单哈希）将其每个项目插入一个二维哈希表，因为它没有办法知道接收方最终对交集中的项目使用哪一个哈希函数。为了确定发送方的最大负载，我们应用一个标准的 “球入仓” 论证。具体来说，当把 个球插入 桶时，我们有

我们的默认假设是，发送方（执行简单散列的人）有一个更大的集合，所以 。在这种情况下， 的上界是 ，概率很大 [51]。

4.2.2 基于置换的散列

独立于精确的散列方案，基于置换的散列 [3] 是一种优化，通过将一个项目的一部分编码到桶索引中来减少存储在散列表中的项目的长度。为了简单起见，我们假设 是 的幂，并且只在与布谷鸟散列有关的情况下描述基于置换的散列。要将一个位串 插入哈希表，我们首先将其解析为 ，其中 的长度等于 。哈希函数 被用来构造位置函数为

我们将在布谷鸟散列中使用它。此外，我们没有像常规布谷鸟散列那样将整个元组 ， 插入散列表，而是只在 指定的位置插入 ，。

在应用基于置换的散列法后，PSI 协议的正确性仍然成立。原因是如果对于 和 ，有 ，那么 ，。此外，如果这些东西在同一位置被发现，那么有 ，所以 ，因此。存储在哈希表中的字符串的长度因此减少了位。完整的散列程序在图 2 中说明。

image-20220524143532474

图 2：哈希程序

  • 输入：接收者输入大小为 的集合 ；发送者输入大小为 的集合 。两个集合都由长度为 的比特串组成。 是公开的。双方都输入整数 ，， 和一组哈希函数 ，，，，。位置函数 是相对于 的 而定义的。

  • 输出：接收者输出一个基于置换的布谷鸟哈希表，其中插入了 中的项目，或 。发送者输出一个基于置换的哈希表，并使用简单哈希和所有位置函数插入 中的项目，或 。

  • 步骤：

    1. [发送方]：令 为一个由 个桶组成的数组，每个桶的容量为 ，值为。对于每个 和 ，发送者对 进行采样，同时 ，并设置 。如果由于一个仓已满而导致抽样失败，发送者输出 。否则，它输出

    2. [接收者]：令 是一个由 个桶组成的数组，每个仓的容量为 ，值为 ，。对于每个 ，接收者

      1. 设置 , 以及 。
      2. 定义并调用函数 ：将 与 的条目交换。如果得到的 ，则递归调用 ，其中 。

      如果对任何 来说，对 的递归调用超过了系统的极限，则接收方停止并输出 。否则，它输出 。

4.2.3 哈希失败

在不太可能发生的情况下，布谷鸟散列算法失败了，它可能会将接收方的一些信息泄露给发送方。为了防止这种情况，我们必须确保布谷鸟散列算法以压倒性的概率成功。虽然存在一些估计布谷鸟散列失败概率的渐进结果 [17, 24]，但隐藏的常数很难精确确定。相反，为了获得最佳参数，我们选择使用经验方法来确定失败概率。我们使用的一般技术与 [50] 相似，但有两个例外：第一，我们省略了一个被称为储藏室的辅助数据结构，因为它与完全同态加密方法不兼容；第二，我们在实验中主要关注 （见下文），而 [50] 关注 。

我们首先固定了由 个仓组成的布谷鸟散列表，并改变要插入的项目 的数量。对于每个 对，我们运行布谷鸟散列算法 次。对于 ，我们发现该算法在实验中从未失败。 为了计算达到 的统计安全级别所需的比率 （即布谷鸟散列失败的概率最多为），我们首先将 设置为一个略大于 1 的值，并逐渐增加，直到我们可以预期散列失败为零。由此我们观察到，当 时， 与比例因子 呈线性增长。

在我们的实验过程中，我们观察到，当 h=2 时，没有储藏室的布谷鸟散列的表现非常差，这在 [50] 中也观察到并详细讨论过，这就是为什么我们将重点转移到 。此外， 的边际收益被简单散列的成本增加所抵消。通过对 的经验数据进行线性回归，我们发现 ，对于 ， 对于 。为了达到 的统计安全水平，因此，在 的情况下，能够被杜鹃散列到 个仓的最大项目数是 。对于 ，相应的最大项目数是 。对于给定的哈希表大小和不同的 值，各自的简单散列参数在表 1 中给出。

image-20220524143830234

表 1：失败概率为 的简单散列仓尺寸上界 ， ， ；见公式（1）。

4.2.4 假项

为了使发送方的简单哈希表均匀地被填满，我们需要在哈希运算后用假项填充每个桶。我们让发送方和接收方从 中固定两个不同的假值，只要它们不作为合法值出现。例如，如果合法值最多有 位，那么我们可以将接收方的假值设为 ，而发送方的假值设为。

4.2.5 哈希到一个较小的表示

在许多情况下，项目的总数 远远小于所有可能的长度为 的字符串的数量 。由于我们协议的性能会随着字符串长度的增加而降低，因此，各方用商定的哈希函数将他们的字符串压缩到一个固定的长度，然后在这些哈希的字符串上执行 PSI 协议是很有好处的。事实上，这是 PSI 社区的一项著名技术。

更确切地说，当总共 个随机字符串被哈希到一个大小为 的域时，发生碰撞的概率大约为 。对于一个统计安全参数 ，我们要求 碰撞发生。因此，压缩后的字符串应该至少有以下长度

现在我们将基于置换的布谷鸟散列法应用于压缩后的字符串，进一步将字符串长度减少到

此外，我们还需要在明文空间中为第 4.2.4 节中讨论的假值多保留两个值。因此，通过选择加密参数 ，使得

我们可以在我们的 PSI 协议中容纳任意长的字符串。

4.2.6 与并行处理相结合

将本节介绍的散列技术与第 4.1 节的批处理技术相结合是很简单的。在接收方将其项目散列到一个大小为 的表中后，它将该表解析为长度为 的 个向量，然后接收方使用批处理对每个向量进行加密，并像往常一样进行。同样地，发送方对其二维哈希表的 列中的每一列执行相同的并行处理步骤，结果是 个明文向量。协议的其余部分保持不变，我们看到在散列技术中加入并行处理，使计算和通信都减少了 倍。

4.3 减少电路深度

通过第 4.1 节和第 4.2 节中讨论的优化，我们的协议已经实现了非常低的通信成本：通常只有几个同态加密的密码文。不幸的是，需要进行同态评估的算术电路的深度仍然是 ，这对于目前已知的完全同态加密方案来说可能是高得令人望而却步。

我们使用两个技巧 -- 窗口和分区 -- 来大大减少这种深度。为了简化论述，我们将讨论这两个技巧如何在基本协议上发挥作用，并简要说明如何将它们与之前的优化结合起来。

4.3.1 窗口化

我们使用标准的窗口技术来降低发送方需要对接收方的同态加密数据进行评估的算术电路的深度，从而实现了有价值的计算 - 通信权衡。

回顾一下，在基本协议中，对于每个项目 ，接收方发送一个密文 给发送方，发送方在中采样一个随机元素 ，同态地评估 ，并将结果发回给接收方。如果接收方发送 的额外幂的加密，发送方可以使用这些幂来评估相同的计算，其深度电路要低得多。更确切地说，对于 比特的窗口大小，接收方对于所有，以及所有，计算，并发送给发送方。例如，当 时，接收方发送的加密。

这种技术使电路深度大大降低。为了看到这一点，我们写道

如果发送方只有 的加密，它最需要计算的是乘积 ，这需要一个深度为 的电路。现在，如果加密的已经给了发送者，那么我们可以把发送者的计算分成两步。首先，发送方计算所有 的 的加密。发送方需要计算的最坏情况是 项的乘积，需要一个深度为的电路。在一个极端的情况下，如果接收方给发送方提供 的所有幂的加密，直到 ，这一步的深度就变成了零。然后，发送方从自己的数据中计算出（）与明文中的系数矢量 的加密的点积。这第二步有一层乘法深度。

窗口化的代价是增加通信量。从接收方到发送方的通信量增加了 ，而从发送方返回接收方的通信量没有变化。

将批处理和散列法与窗口法结合起来是很容易的。唯一的区别是，批处理和散列法能有效地将发送者的集合大小减少近 倍。更确切地说，电路的深度变成了，其中 如图 2。在没有窗口化的情况下，批处理和散列将整个集合 编码为一个大小为 的散列表，产生 个密文，以传达给发送者。在使用窗口化的情况下，这将扩展为个密文。

最后，我们注意到，窗口技术的安全性是由底层全同态加密方案的 IND-CPA 安全性保证的。

4.3.2 分区

另一种减少电路深度的方法是让发送方将其集合划分为 个子集，并对每个子集执行一次 PSI 协议。在基本协议中，这将发送方的电路深度从 减少到 ，代价是发送方到接收方的返回通信量增加了 倍。

分区可以自然地与窗口化结合起来，这样做还有一个好处，就是减少同态操作的数量。回顾一下第 4.3.1 节，发送方需要为接收方的每个项目 计算所有幂 。有了分区，发送方只需要计算的加密，这就使接收方的每一个项目都能得到加密。它可以为 个分区中的每个分区重新使用。因此，在分区和开窗的情况下，发件人在第 4.3.1 节中描述的第一步的计算成本减少了一个系数 ，而第二步的成本保持不变。

我们可以通过以下方式将批处理和散列与分区相结合。发送方像往常一样执行它的那部分散列程序（图 2），但是把它的桶（每个大小为）的内容分成同等大小的 部分，结果是 个表，每个的桶大小约为 。然后，它通过第 4.1、4.2 和 4.3.1 节中描述的改进，使用每一个 哈希表执行 PSI 协议。现在发送方的电路深度减少到 ，其中如图 2 所示。从发送方到接收方的通信是 个密文。

我们要注意的是，为了维护发送方的安全，在使用简单的散列法将其项目插入散列表后，发送方必须以统一的随机方式对桶的内容进行分割，包括值为 ， 的空位置。由于在散列程序中（图 2），发送方在每个仓内的随机位置插入其项目，正确的分区可以通过使用任何确定的分区方法将每个仓的内容均匀地分割成 个子集来实现。

4.4 通过模数转换减少回复大小

最后，我们采用模数转换（见 [12]），有效地减少了响应密码文的大小。模数转换是基于格的全同态加密方案中一个著名的操作。它是一个公开的操作，它将一个加密参数为 的密码文转换为一个加密相同明文的密文，但参数 。由于 FHE 密码文的大小与对数 呈线性关系，模数转换将密码文的大小减少了一个 的系数。这个技巧允许发送方在向接收方发送之前 "压缩" 返回的密码文。在实践中，我们能够将返回的密码文减少到其原始大小的约 15-20%。我们注意到，只要在设置时确定了较小的模数 ，该协议的安全性就会被微不足道地保留下来。

5 完整的协议和安全证明

5.1 正式的描述

我们在图 4 中详细介绍了完整的协议，给定了一个安全的全同态加密方案和电路隐私。该协议的理想功能在图 3 中给出。

我们在标准的基于半诚实的模拟范式中证明安全性。宽泛地说，我们说图 4 的协议 安全地实现了功能 ，如果它是正确的，并且存在两个模拟器（PPT 算法）、，具有以下特性。模拟器 将接收者的集合和交集作为输入，需要为协议的执行生成一个与接收者对真实交互的看法不可区分的记录。 的定义与此类似，只是不把交集作为输入。关于半诚实设置中基于模拟的安全的正式定义，我们请读者参考 [40]。

image-20220524144057843
图 3：理想的功能 FPSI，用于单边输出的私有集相交
  • 参数：两方分别表示为发送方和接收方，其项目集的比特长度为 。接收方的集合大小为 ；发送方的集合大小为 。 表示协议实例的会话 ID。
  • 功能：从接收方输入 ，从发送方输入 ，其中 ，。该功能将 发送给接收方，而不发送给发送方。
image-20220524144227892
图 4：完整的协议

  • 输入：接收方输入尺寸为 的集合 ；发送方输入尺寸为 的集合 ，， 和 都是公开的。 和 分别表示计算和统计安全参数。

  • 输出：接收方输出 ；发送方什么也不输出。

  • 步骤：

    1. 进行散列：哈希参数 、 和 是商定的，这样简单的哈希 个球进入 个仓，最大容量为 ，同时使用布谷鸟哈希 个球入仓，成功概率大于等于 。

      1. 哈希到较短的字符串：令 。如果 ，那么双方都把他们的集合哈希到一个较小的表示。首先，对随机哈希函数 ：，，进行采样。令 ，。用 代替 执行协议的其余部分，并输出 , 中的相应项目作为交集。
      2. 哈希到桶中：双方以参数 、 和 和随机抽样的哈希函数作为输入，执行图 2 的哈希程序。发送方用集合 执行步骤 1，得到 ，接收方用集合 执行步骤 2，得到 。即执行布谷鸟哈希。

    2. 选择 FHE 参数：双方就具有电路隐私的 IND-CPA 安全 FHE 方案的参数 达成一致。他们选择 足够大，以便 。

    3. 选择电路深度参数：双方就窗口参数 和分区参数 达成一致，以最小化整体成本。

    4. 发送方预处理集合 ：

      1. 分区：发送方将其表 纵向（即按列）划分为 个子表 ，每个表都有 列。
      2. 计算系数：对于每个子表的每一行 ，发送者用多项式 的系数替换行 ，即用 替换 。
      3. 批处理：对于从上一步得到的每个子表，发送方将其每一列解读为一个长度为 的矢量，其元素在 中。然后，发送方将每个向量批处理为 个明文多项式。结果是，第 个子表被转化为 个多项式 。

    5. 接收方加密集合 ：

      1. 批处理：接收方将 解释为一个长度为 的矢量，元素在 中。它把这个向量分成若干个明文多项式。
      2. 窗口化：对于在步骤 中计算的每个分批明文多项式 ，接收方计算分量的第 次幂 ，其中（）。
      3. 加密：接收者使用 对每个这样的幂进行加密，获得 个密文集合。接收方将这些密文发送给发送方。

    6. 发送方计算交集：

      1. 同态计算所有幂的加密：对于每个密文集合 ，发送者同态地计算一个矢量 ，其中 是一个同态的密文加密。最后，发送方获得 个向量。

      2. 同态计算点积：发送方同态计算

        可选择对密文 进行模数转换以减少其大小，并将其送回给接收方。

    7. 解密并获得结果：对于每个 ，接收方对其收到的所有密文进行解密，并将 个结果向量串联成一个长度为 的向量 。最后，接收方输出

定理 5.1：图 4 中的协议是半诚实环境下 的安全协议。

证明：很容易看出，该协议正确计算交集的条件是散列程序成功，这以压倒性的概率 发生。

我们从一个腐败的接收者开始，并证明 的存在。为了便于阐述，我们将假设模拟器 / 协议的参数由 组成，这些参数是固定的和公开的，并且使用散列到一个较小的表示（第 4.2.5 节）。然后我们将定义接收方的模拟器 如下。 计算集合 ，并使用修改过的散列程序将其元素布谷鸟式散列到一个大小为 的表中。修改后的结果是，如果一个元素 在 中，那么就插入一个 ，否则就插入 中的一个随机非零元素。散列结束后， 将 中的随机非零元素插入剩余的空槽中。接下来， 再创建 个相同大小的表，并将 中的随机非零元素填入其中。然后，它在所有 个表之间随机地将插入匹配槽中的值进行排列组合。最后，它将每个表分批放入 个 FHE 明文多项式中，并将它们同态地加密成 个密文。由此产生的 密码文将作为接收器的模拟视图。由于底层全同态加密方案的电路隐私假设，在协议的实际执行中，这个视图与接收者的视图是不可区分的。

腐败的发送者的情况是直接的。模拟器 可以生成新的 0 的加密，以取代步骤 5 中的加密。根据全同态加密方案的 IND-CPA 安全性，这个结果与真实协议中的发件人的观点是不可区分的。

5.2 讨论

5.2.1 功能隐私

虽然我们的协议（图 4）假设了一个具有电路隐私的全同态加密方案，但在实践中，用分级全同态加密来实例化它要有效得多（回顾第 2.3 节），即选择足够大的加密参数来避免昂贵的引导操作。 这并不改变协议的安全属性，因为加密参数的选择纯粹是基于公共参数 。

虽然电路隐私可以通过使用例如 [19] 的技术在完全同态加密中实现，但在实践中，稍弱的（统计）函数隐私概念 [27] 就足够了，而且在使用重新随机化和噪声淹没的平坦设置中更容易实现，其中发送者通过同态地添加一个具有非常大噪声的零的加密来重新随机化输出密码文 [19，25]。一个标准的 "污点定理"（见例如 [5]）意味着，为了在不同执行的输出密码文之间实现 的统计距离，只需添加噪音为 位的零的加密，比计算的原始输出的噪音的上限大。我们使用了 [14] 中的启发式结果来约束淹没前输出密码文的噪音量。

5.2.2 恶意行为

当考虑到恶意行为时，我们的协议面临几个挑战。最值得注意的是，发送方有能力在接收方的同态加密数据集上计算一个任意的函数。虽然发送方不能直接从密码文本中学习额外的信息，但它能够恶意地影响输出的正确性，例如强迫交集 / 输出为接收方的全集，或者更普遍的是 。有效地防止发送方的这种行为似乎极具挑战性。

对于恶意接收者的情况，我们只需要考虑接收者可能引起的潜在泄漏（发送者没有输出）。首先，由于接收器有能力填补布谷鸟哈希表的空位，因此它可能提供一个大小大于 的集合。此外，由于接收方可能提供比预期更多噪音的密码文，函数隐私可以通过噪音泛滥轻松实现的论点不再成立。因此，响应的密码文的噪声水平可能取决于发送者的集合，从而泄露额外的信息。然而，在一般情况下，我们认为该协议为大多数实际应用提供了合理的保护，以防止恶意接收者。我们将对恶意设置和潜在的对策进行更正式的分析留给未来的工作。

5.2.3 当接收者持有较大的集合时

到目前为止，我们已经做了一个假设，即接收方的集合大小比发送方的集合大小小很多。在此我们指出，我们的协议可以稍作修改，以处理相反的情况，即接收方持有较大的集合。我们的想法是，双方可以在执行我们的协议时互换角色，直到最后一步。在这一点上，接收方（现在一直扮演发送方的角色）持有一个向量 的加密。它对一个随机的明文向量 进行采样，并向发送者发回一个 的加密值。发送方对这个值进行解密，并将明文向量 发回给接收方，接收方可以计算出最终结果 。这个协议在半诚实的情况下仍然是安全的，通信在较小的集合中保持线性，在较大的集合中保持对数。

6 执行和绩效

6.1 性能成果

我们实现了图 4 中描述的 PSI 协议。对于完全同态加密，我们使用 SEAL v2.1 [38]，它在 C++ 中实现了 Fan-Vercauteren 方案 [21]。我们使用的 SEAL 的参数在表 2 中给出，还有它们的计算安全等级 ，是根据目前已知的最佳攻击 [1，2] 估计的。标有 "DBC" 的一栏是指 SEAL 中的分解位数参数。我们注意到，这些参数对于我们进行的特定计算是高度优化的。

我们在表 3 中给出了我们的协议在 4、16 和 64 个线程的单线程和多线程执行中的详细计算性能结果。由于接收方的计算量与发送方的计算量相比通常较小，因此我们限制了接收方的单线程执行。不过，值得指出的是，如果有多线程，接收方的计算也会大大受益。表 4 给出了我们实验中的通信成本。我们选择了一个统计安全级别 ，字符串长度 位。

该基准机有两个 18 核英特尔至强 CPU E52699 v3 @ 2.3GHz 和 256GB 的内存。我们使用这台单机进行所有测试，并使用 Linux tc 命令模拟网络延迟和带宽。具体来说，我们考虑一个局域网设置，双方通过本地主机连接，吞吐量为 10Gbps，往返时间（RTT）为 0.2ms。我们还考虑了三种广域网设置，分别为 100Mbps、10Mbps 和 1Mbps 带宽，每一种都有 80ms 的往返时间。所有时间都是以 10 次试验的平均值报告的。

image-20220524145602690

表 2：SEAL v2.1 的加密参数集。安全性估计是基于 [1，2]

image-20220524145638448

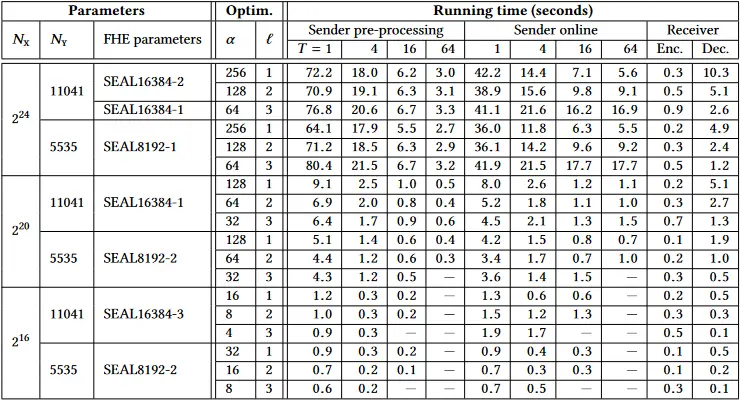
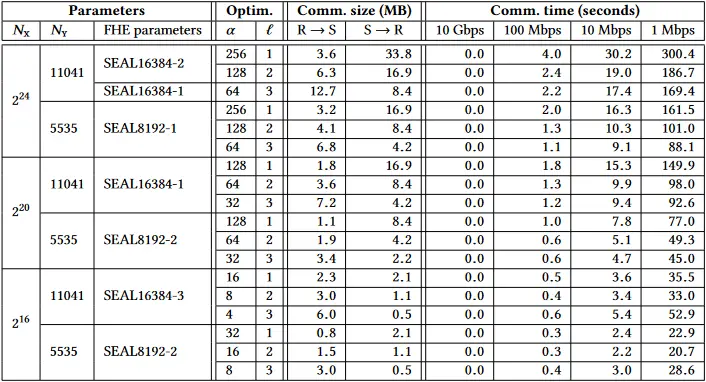
表 3: 我们的协议在 线程下的运行时间（秒）； ， ， 。由于我们通过在线程之间平均分配 分区来实现多线程所以 不会带来性能上的好处。这些情况在表中用 " " 表示。

image-20220524145805342

表 4：我们协议的通信成本（MB）； ， ， 。10Gbps 网络假设 RTT 为 0.2ms，其他使用 80ms RTT。 和 表示从接收方到发送方，以及从发送方到接收方的通信。

6.2 与 Pinkas 等人的比较

我们的主要比较点是 Pinkas 等人的 PSI 协议 [50]，在该协议中，作者同时考虑了对称集合大小的情况，以及接收方的集合明显小于发送方的情况。虽然我们的协议可以很容易地处理对称集的大小，但与 [50] 相比，我们的主要优势在于非对称设置，也就是我们现在关注的。为了更容易比较这两个协议，我们在同一台机器上运行它们，并在表 5 中总结了并列的总运行时间。我们选择评估 ，，，， 的集合大小的性能，以最大限度地利用密码文本批处理，在第 4.1 节中描述。在第 4.2.3 节中， 的大小被确定为能够保证 的统计安全水平的最大尺寸。如果需要与 [50] 中报告的运行时间进行直接比较，读者可以随意将我们的集合大小 四舍五入以匹配其中的大小。

在比较这两个协议时，我们发现，当发送者的集合大小大于 时，我们的通信成本扩展得更好。例如，当考虑到 位的字符串， ， 时，我们的协议发送 5.6MB，而同样的 ， 参数应用于 [50]，导致 30.4MB 的通信 --5.4 倍的改进。将 进一步增加到 ，我们的协议只需要 11.0MB 的通信，而 [50] 需要超过 480MB--43.7 倍的改进。此外，继续增加发送方的集合大小会带来更大的通信优势。

当在单线程局域网设置中计算大小为 和 的集合的交集时，我们的协议需要 8.6 秒。使用相同的参数评估 [50] 的协议，其执行时间为 3.1 秒。虽然 [50] 在这个特定的环境中比我们的协议更快，但它也需要 5.4 倍的通信，并在各方之间平均分配计算成本。也就是说，每一方都进行了 的操作。相比之下，我们的协议对接收方的计算能力要求很低。

由于我们的协议在非对称集大小的设置中实现了比 [50] 更低的通信量，所以随着我们减少网络带宽，我们获得了更好的性能。为了清楚地证明这一点，我们考虑了其他几个模拟广域网设置的网络环境。特别是，我们将各方限制在一个 100Mbps、10Mbps 和 1Mbps 的网络中，往返时间为 80ms。在这些环境中，我们的协议除少数例外情况外都优于 [50]。也就是说，在单线程的 100Mbps 设置中， ， ，我们的协议需要 107.2 秒，而 [50] 需要 87.9 秒。然而，我们的协议在多线程设置中得到了更大的加速，当发送者使用 4 个线程时，我们的运行时间减少到 36.7 秒。另一方面，[50] 在相同的集合大小下，双方使用 4 个线程，需要 65.5 秒 -- 与我们的协议相比，速度降低了近 1.8 倍。随着我们进一步降低带宽，差异变得更加明显。在 1Mbps 的单线程设置中， ， ，我们的协议需要 211.1 秒，而 [50] 需要 4080.6 秒，这是运行时间的 19.3 倍。当利用 4 个线程时，我们的运行时间减少到 132.7 秒，而 [50] 需要 4064.3 秒 --30.6 倍的改进。

我们还考虑了当发送方使用 4 个以上的线程时，我们协议的运行时间。当在局域网设置中允许 16 个线程时，我们的运行时间在 ， 时减少到 16.9 秒。另一方面，[50] 经历了比 4 个线程更少的加速，当用 16 个线程执行时， 只需要 20 多秒。这表明，即使在局域网环境下，当发送方使用至少 16 个线程时，我们的协议也能胜过 [50]。

我们协议的一个重要特性是接收方所需的工作量相对较小。在许多应用中，接收方的计算能力明显低于发送方。这在发现联系人的应用中最为明显，在这种应用中，接收方可能是一部手机，而发送方可以在一个计算能力不高的大型数据中心运行。例如，表 3 中的参数 ， ， 显示，对于 和 项之间的交集，接收方只需要进行 1.7 秒的计算，而有 16 个线程的服务器需要 18 秒，通信总量为 11MB，不到 2012 年 iOS 应用程序平均下载量的一半 [52]，是 2015 年美国智能手机平均每日移动数据用量的十分之一 [20]。相比之下，[50] 需要 480MB 的通信量 -- 增加了 44 倍 -- 而且接收器的计算负荷明显更高，需要 5000 万次哈希表查询和几千个不经意传输。

6.3 与 Kolesnikov 等人比较

我们还将我们的协议与 Kolesnikov 等人 [37] 的协议进行比较，后者优化了不经意传输的使用。虽然他们的结果确实改善了大项目对称集的运行时间，但我们发现，当应用于我们的设置时，他们的改进没有提供什么好处，而且被 [50] 采用的其他优化所抵消。特别是，[50] 考虑了一个不同的不经意传输优化，它在短字符串上更有效，并且还优化了布谷鸟散列对非对称集大小的设置。

这些设计决定导致 [37] 在与参数为 、 、 的 和 大小的集合相交时，需要比 [50] 多 2 倍的通信，比我们的协议多 87 倍。在对 [37] 进行基准测试时，我们发现通信量实际上比他们的理论极限大 1.5 倍。[37] 的理论通信复杂度是： 其中， 是布谷鸟散列中的储藏室大小， 是伪随机码的宽度， 是 OPRF 输出的大小， 与布谷鸟散列的利用率有关。[50] 的通信复杂度也遵循相同的等式，但由于更优化的不经意传输子协议，其 更小。另一方面，我们的协议需要 位的通信，其中 是一个用于密码文本扩展的小常数， 是字符串长度， 与没有存储的布谷鸟散列的利用率有关。例如，当 ， 时，我们的协议只需要 12.5MB 的通信，而 [37] 在这种情况下的经验通信几乎大了 115 倍。

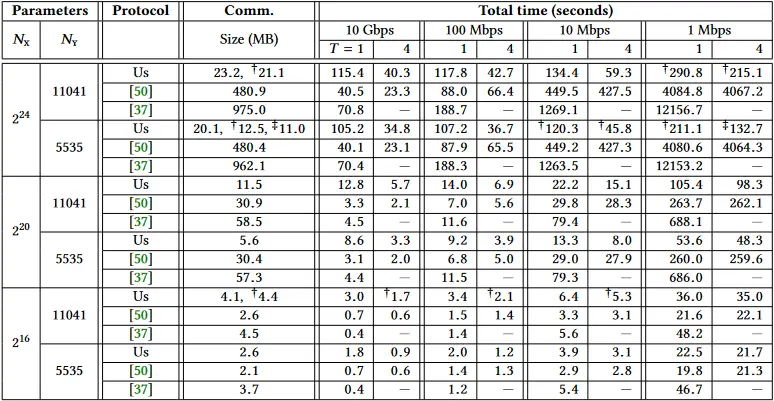
与 [50] 和我们的协议相比，在广域网设置中，通信的增加转化为运行时间的增加。例如，当在 10Mbps 的连接上与 和 个项目相交时，我们的协议要快 57 倍以上，而 [50] 只快 3 倍。表 5 中总结了总的运行时间，以便于与我们的协议和 [50] 进行比较。由于 [37] 的实现不支持多线程，我们只列出了 的结果。

image-20220524150938986

表 5：在 线程； ， ， 的情况下，将我们的协议与 [50] 和 [37] 的总通信成本（MB）和运行时间（秒）进行比较。10Gbps 网络假设 RTT 为 0.2ms，其他网络使用 80ms RTT。由于 [37] 实施的限制，只显示了单线程的结果。[37] 的通信成本是基于他们论文中提供的方程式；据观察，经验通信是 1.5 倍以上。

7 结论

尽管自 Craig Gentry 在 2009 年的开创性工作以来，全同态加密方案有了巨大的进步，但许多人仍然认为它对于实际使用情况来说太昂贵了。然而，在本文中，我们使用 Fan-Vercauteren 方案构建了一个实用的私有集相交协议，采用并结合了全同态加密和 PSI 的前沿工作的优化。我们认为我们的协议对于隐私联系人发现的使用情况特别有趣，它实现了非常低的通信开销：将一个 5 千项的集合与一个 1600 万项的集合相交，大约需要 12MB，这比以前最先进的协议要低很多。我们认为我们的工作是探索将完全同态加密应用于私有集合相交的可能性的第一步，并期待着进一步的讨论和优化。

参考文献

  1. Martin R Albrecht. 2017. On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL. In Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, 103–129.

  2. Martin R. Albrecht, Rachel Player, and Sam Scott. 2015. On the concrete hardness of Learning with Errors. J. Mathematical Cryptology 9, 3 (2015), 169–203. http://www.degruyter.com/view/j/jmc.2015.9.issue-3/jmc-2015-0016/ jmc- 2015- 0016.xml

  3. Yuriy Arbitman, Moni Naor, and Gil Segev. 2010. Backyard cuckoo hashing: Constant worst-case operations with a succinct representation. In Foundations of Computer Science (FOCS), 2010 51st Annual IEEE Symposium on. IEEE, 787–796.

  4. Frederik Armknecht, Colin Boyd, Christopher Carr, Kristian Gjøsteen, Angela Jäschke, Christian A Reuter, and Martin Strand. 2015. A guide to fully homomorphic encryption. Technical Report. IACR Cryptology ePrint Archive (2015/1192).

  5. Gilad Asharov, Abhishek Jain, Adriana López-Alt, Eran Tromer, Vinod Vaikuntanathan, and Daniel Wichs. 2012. Multiparty computation with low communication, computation and interaction via threshold FHE. In Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, 483–501.

  6. Giuseppe Ateniese, Emiliano De Cristofaro, and Gene Tsudik. 2011. (If) Size Matters: Size-Hiding Private Set Intersection. In Public Key Cryptography - PKC 2011 - 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, March 6-9, 2011. Proceedings (Lecture Notes in Computer Science), Dario Catalano, Nelly Fazio, Rosario Gennaro, and Antonio Nicolosi (Eds.), Vol. 6571. Springer, 156–173. https://doi.org/10.1007/978-3-642-19379-8_10

  7. Josh Benaloh and Michael de Mare. 1994. One-Way Accumulators: A Decentralized Alternative to Digital Signatures. Springer Berlin Heidelberg, Berlin, Heidelberg, 274–285. https://doi.org/10.1007/3-540-48285-7_24

  8. Joppe W Bos, Kristin Lauter, Jake Loftus, and Michael Naehrig. 2013. Improved security for a ring-based fully homomorphic encryption scheme. In Cryptography and Coding. Springer, 45–64.

  9. Tatiana Bradley, Sky Faber, and Gene Tsudik. 2016. Bounded size-hiding private set intersection. In International Conference on Security and Cryptography for Networks. Springer, 449–467.

  10. Tatiana Bradley, Sky Faber, and Gene Tsudik. 2016. Bounded Size-Hiding Private Set Intersection. In Security and Cryptography for Networks - 10th International Conference, SCN 2016, Amalfi, Italy, August 31 - September 2, 2016, Proceedings (Lecture Notes in Computer Science), Vassilis Zikas and Roberto De Prisco (Eds.), Vol. 9841. Springer, 449–467. https://doi.org/10.1007/978-3-319-44618-9_24

  11. Zvika Brakerski, Craig Gentry, and Shai Halevi. 2013. Packed ciphertexts in LWE-based homomorphic encryption. In Public-Key Cryptography–PKC 2013. Springer, 1–13.

  12. Zvika Brakerski, Craig Gentry, and Vinod Vaikuntanathan. 2012. (Leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference. ACM, 309–325.

  13. Zvika Brakerski and Vinod Vaikuntanathan. 2014. Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 43, 2 (2014), 831–871.

  14. Ana Costache and Nigel P Smart. 2016. Which Ring Based Somewhat Homomorphic Encryption Scheme is Best?. In Cryptographers’ Track at the RSA Conference. Springer, 325–340.

  15. Dana Dachman-Soled, Tal Malkin, Mariana Raykova, and Moti Yung. 2009. Efficient Robust Private Set Intersection. In Proceedings of the 7th International Conference on Applied Cryptography and Network Security (ACNS ’09). SpringerVerlag, Berlin, Heidelberg, 125–142. https://doi.org/10.1007/978-3-642-01957-9_8

  16. Luc Devroye and Pat Morin. 2003. Cuckoo hashing: further analysis. Inform. Process. Lett. 86, 4 (2003), 215–219.

  17. Martin Dietzfel 桶 ger, Andreas Goerdt, Michael Mitzenmacher, Andrea Montanari, Rasmus Pagh, and Michael Rink. 2010. Tight thresholds for cuckoo hashing via XORSAT. In International Colloquium on Automata, Languages, and Programming. Springer, 213–225.

  18. Changyu Dong, Liqun Chen, and Zikai Wen. 2013. When private set intersection meets big data: an efficient and scalable protocol. In Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. ACM, 789–800.

  19. Léo Ducas and Damien Stehlé. 2016. Sanitization of FHE ciphertexts. In Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, 294–310.

  20. Ericsson. 2016. Ericsson Mobility Report: ON THE PULSE OF THE NETWORKED SOCIETY. Stockholm, Sweden (2016).

  21. Junfeng Fan and Frederik Vercauteren. 2012. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Report 2012/144. (2012). http://eprint.iacr.org/.

  22. Dimitris Fotakis, Rasmus Pagh, Peter Sanders, and Paul Spirakis. 2003. Space efficient hash tables with worst case constant access time. In Annual Symposium on Theoretical Aspects of Computer Science. Springer, 271–282.

  23. Michael J. Freedman, Kobbi Nissim, and Benny Pinkas. 2004. Efficient Private Matching and Set Intersection. In Advances in Cryptology - EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, May 2-6, 2004, Proceedings (Lecture Notes in Computer Science), Christian Cachin and Jan Camenisch (Eds.), Vol. 3027. Springer, 1–19. https://doi.org/10.1007/978- 3- 540- 24676- 3_1

  24. Alan Frieze, Páll Melsted, and Michael Mitzenmacher. 2009. An analysis of random-walk cuckoo hashing. In Approximation, Randomization, and Com 桶 atorial Optimization. Algorithms and Techniques. Springer, 490–503.

  25. Craig Gentry. 2009. Fully homomorphic encryption using ideal lattices.. In STOC, Vol. 9. 169–178.

  26. Craig Gentry, Shai Halevi, and Nigel P Smart. 2012. Homomorphic evaluation of the AES circuit. In Advances in Cryptology–CRYPTO 2012. Springer, 850–867.

  27. Craig Gentry, Shai Halevi, and Vinod Vaikuntanathan. 2010. i-hop homomorphic encryption and rerandomizable Yao circuits. In Annual Cryptology Conference. Springer, 155–172.

  28. Craig Gentry, Amit Sahai, and Brent Waters. 2013. Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based. In CRYPTO (1) (Lecture Notes in Computer Science), Ran Canetti and Juan A. Garay (Eds.), Vol. 8042. Springer, 75–92. https://doi.org/10.1007/ 978- 3- 642- 40041- 4

  29. Ran Gilad-Bachrach, Nathan Dowlin, Kim Laine, Kristin Lauter, Michael Naehrig, and John Wernsing. 2016. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy. In Proceedings of The 33rd International Conference on Machine Learning. 201–210.

  30. Carmit Hazay and Yehuda Lindell. 2008. Efficient protocols for set intersection and pattern matching with security against malicious and covert adversaries. In Theory of Cryptography Conference. Springer, 155–175.

  31. Carmit Hazay and Kobbi Nissim. 2010. Efficient set operations in the presence of malicious adversaries. In International Workshop on Public Key Cryptography. Springer, 312–331.

  32. Carmit Hazay and Kobbi Nissim. 2012. Efficient set operations in the presence of malicious adversaries. Journal of cryptology 25, 3 (2012), 383–433.

  33. Yan Huang, David Evans, and Jonathan Katz. 2012. Private set intersection: Are garbled circuits better than custom protocols?. In NDSS.

  34. Bernardo A. Huberman, Matt Franklin, and Tad Hogg. 1999. Enhancing Privacy and Trust in Electronic Communities. In In Proc. of the 1st ACM Conference on Electronic Commerce. ACM Press, 78–86.

  35. Yuval Ishai, Joe Kilian, Kobbi Nissim, and Erez Petrank. 2003. Extending oblivious transfers efficiently. In Annual International Cryptology Conference. Springer, 145161.

  36. Seny Kamara, Payman Mohassel, Mariana Raykova, and Seyed Saeed Sadeghian. 2014. Scaling Private Set Intersection to Billion-Element Sets. In Financial Cryptography and Data Security - 18th International Conference, FC 2014, Christ Church, Barbados, March 3-7, 2014, Revised Selected Papers (Lecture Notes in Computer Science), Nicolas Christin and Reihaneh Safavi-Naini (Eds.), Vol. 8437. Springer, 195–215. https://doi.org/10.1007/978-3-662-45472-5_13

  37. Vladimir Kolesnikov, Ranjit Kumaresan, Mike Rosulek, and Ni Trieu. 2016. Efficient Batched Oblivious PRF with Applications to Private Set Intersection. Cryptology ePrint Archive, Report 2016/799. (2016). http://eprint.iacr.org/2016/799.

  38. Kim Laine, Hao Chen, and Rachel Player. 2016. Simple Encrypted Arithmetic Library - SEAL (v2.1). Technical Report. Microsoft Research. https://www.microsoft.com/en-us/research/publication/ simple- encrypted- arithmetic- library- seal- v2- 1/

  39. Mikkel Lambaek. 2016. Breaking and Fixing Private Set Intersection Protocols. Cryptology ePrint Archive, Report 2016/665. (2016). http://eprint.iacr.org/2016/ 665.

  40. Yehuda Lindell. 2016. How To Simulate It - A Tutorial on the Simulation Proof Technique. Cryptology ePrint Archive, Report 2016/046. (2016). http://eprint. iacr.org/2016/046.

  41. Adriana López-Alt, Eran Tromer, and Vinod Vaikuntanathan. 2012. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In Proceedings of the forty-fourth annual ACM symposium on Theory of computing. ACM, 1219–1234.

  42. Vadim Lyubashevsky, Chris Peikert, and Oded Regev. 2010. On Ideal Lattices and Learning with Errors over Rings. In Advances in Cryptology - EUROCRYPT 2010, 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, May 30 - June 3, 2010. Proceedings (Lecture Notes in Computer Science), Henri Gilbert (Ed.), Vol. 6110. Springer, 1–23. https://doi.org/10.1007/978- 3- 642- 13190- 5_1

  43. Moxie Marlinspike. 2014. The Difficulty Of Private Contact Discovery. A company sponsored blog post. (2014). https://whispersystems.org/blog/ contact- discovery/.

  44. C. Meadows. 1986. A More Efficient Cryptographic Matchmaking Protocol for Use in the Absence of a Continuously Available Third Party. In 1986 IEEE Symposium on Security and Privacy. 134–134. https://doi.org/10.1109/SP.1986. 10022

  45. Michael Naehrig, Kristin E. Lauter, and Vinod Vaikuntanathan. 2011. Can homomorphic encryption be practical?. In Proceedings of the 3rd ACM Cloud Computing Security Workshop, CCSW 2011, Chicago, IL, USA, October 21, 2011, Christian Cachin and Thomas Ristenpart (Eds.). ACM, 113–124. https://doi.org/10.1145/ 2046660.2046682

  46. Michele Orrù, Emmanuela Orsini, and Peter Scholl. 2017. Actively Secure 1-outof-N OT Extension with Application to Private Set Intersection. In Cryptographers’ Track at the RSA Conference. Springer, 381–396.

  47. Rasmus Pagh and Flemming Friche Rodler. 2001. Cuckoo hashing. In European Symposium on Algorithms. Springer, 121–133.

  48. Benny Pinkas, Thomas Schneider, Gil Segev, and Michael Zohner. 2015. Phasing: Private set intersection using permutation-based hashing. In 24th USENIX Security Symposium (USENIX Security 15). 515–530.

  49. Benny Pinkas, Thomas Schneider, and Michael Zohner. 2014. Faster Private Set Intersection Based on OT Extension.. In Usenix Security, Vol. 14. 797–812.

  50. Benny Pinkas, Thomas Schneider, and Michael Zohner. 2016. Scalable Private Set Intersection Based on OT Extension. Cryptology ePrint Archive, Report 2016/930. (2016). http://eprint.iacr.org/2016/930.

  51. Martin Raab and Angelika Steger. 1998. “Balls into Bins” – A Simple and Tight Analysis. In International Workshop on Randomization and Approximation Techniques in Computer Science. Springer, 159–170.

  52. ABI Research. 2012. Average Size of Mobile Games for iOS Increased by a Whopping 42% between March and September. London, United Kingdom (2012).

  53. Peter Rindal and Mike Rosulek. 2016. Improved Private Set Intersection against Malicious Adversaries. Cryptology ePrint Archive, Report 2016/746. (2016). http://eprint.iacr.org/2016/746.

  54. Ronald L Rivest, Len Adleman, and Michael L Dertouzos. 1978. On data banks and privacy homomorphisms. Foundations of secure computation 4, 11 (1978), 169–180.

  55. Nigel P Smart and Frederik Vercauteren. 2014. Fully homomorphic SIMD operations. Designs, codes and cryptography 71, 1 (2014), 57–81.