Scalable Private Set Intersection Based on OT Extension

发表于 2022-06-07 更新于 2022-12-12 分类于论文翻译

基于 OT 扩展的可扩展隐私集合求交集

隐私集合求交集（PSI）允许双方计算他们的集的交集，而不透露不在交集中的项目的任何信息。这是研究得最好的安全计算应用之一，许多 PSI 协议已经被提出。然而，现有的 PSI 协议的多样性使得我们很难确定在各自场景中表现最好的解决方案，特别是由于它们没有在相同的环境中进行比较。此外，现有的 PSI 协议比不安全的朴素散列解决方案慢几个数量级，而这是在实践中使用的。

在这篇文章中，我们回顾了在 PSI 协议方面取得的进展，并对各种安全模型中的现有协议进行了概述。然后，我们关注对半诚实对手安全的 PSI 协议，并利用不经意传输（OT）扩展的最新效率改进，对以前的 PSI 协议提出重大优化，并提出一种运行时间优于现有协议的新 PSI 协议。我们通过在同一平台上实现所有协议，从理论上和实验上比较了协议的性能，对在特定环境下使用哪种协议提出了建议，并通过与目前采用的不安全的朴素散列协议进行比较，评估了 PSI 协议的进展。我们通过处理两个各有 10 亿元素的集合来证明我们新的 PSI 协议的可行性。

1 介绍

隐私集合求交集（PSI）允许分别持有集合和的两方和确定相交的，而不透露不在相交处的元素的任何信息。基本的 PSI 功能可用于两方希望对他们必须保密的数据库表进行操作的应用中，例如，客户或病人的偏好、属性或个人记录的私人列表。PSI 被用于几个研究项目，用于保护隐私的计算功能，如社交网络中的关系路径发现（Mezzour 等人，2009 年），僵尸网络检测（Nagaraja 等人，2010 年），完全测序的人类基因组测试（Baldi 等人，2011 年），接近性测试（Narayanan 等人，2011 年）或网络游戏中的作弊者检测（Bursztein 等人，2011 年）。

PSI 是一个非常活跃的研究领域，已经有很多关于 PSI 协议的建议。大量建议的协议使得进行全面的交叉评价变得非同小可。更加复杂的是，许多协议设计没有被实施和评估，在不同的假设和观察下被分析，并且经常在整体运行时间上被优化，而忽略了其他相关因素，如通信。此外，即使已经引入了几个 PSI 协议，需要计算隐私敏感列表的交集的实际应用往往使用不安全的解决方案。安全解决方案接受度低的原因是，除其他外，现有方案的效率低下，其开销比不安全的解决方案多出两个数量级。

在这篇文章中，我们概述了现有的高效 PSI 协议，优化了现有的 PSI 协议，并描述了一种基于高效不经意传输（OT）扩展的新 PSI 协议。我们在同一平台上比较了所有协议的理论和经验性能，并评估了它们与实践中使用的不安全的基于哈希的解决方案相比的成本。我们表明，与实践中使用的解决方案相比，我们的新 PSI 协议实现了合理的开销。

1.1 应用

我们工作的动力来自于几个需要 PSI 功能的实际应用。在下文中，我们列出了其中的三个应用：

衡量广告转化率：衡量广告转化率是通过比较看过广告的人和完成交易的人的名单来进行的。这些名单分别由广告商（例如谷歌或 Facebook）和商家持有。通常有可能在两端识别用户，使用诸如信用卡号码、电子邮件地址之类的标识。一个忽视隐私的简单解决方案是，一方向另一方披露其客户名单，然后由后者计算出必要的统计数据。另一个选择是在双方之间运行一个 PSI 协议。(该协议可能应该是 PSI 的一个变体，例如，计算看过广告的客户的总收入）。这种协议可以从基本的 PSI 协议中衍生出来）。事实上，Facebook 正在与 Datalogix、Epsilon 和 Acxiom 等公司运行这种类型的服务，这些公司拥有美国大部分会员卡持有人的交易记录。我们的结果表明，即使对于大型数据集，也可以使用安全协议进行计算。

安全事件信息共享：安全事件处理人员可以从信息共享中获益，因为这为他们在事件发生期间提供了一个全局视图。然而，事件数据往往是敏感的，而且可能是令人尴尬的。共享的信息可能会泄露提供信息的公司或其客户的业务信息。因此，信息的共享通常是相当稀少的，并使用法律协议进行保护。自动化的大规模共享将提高安全性，事实上，已经有了这方面的工作，如 IETF 管理事件轻量级交换（MILE）工作。许多应用于共享数据的计算都是计算交叉点及其变体。应用 PSI 来执行这些计算可以简化信息共享的法律问题。高效的 PSI 协议将使其能够经常和大规模地运行。

隐私的联系人发现：当一个新的用户注册到一个服务时，识别当前的注册用户也是新用户的联系人往往是很重要的。这个操作可以通过简单地将用户的联系人列表透露给服务来完成，但也可以通过在用户的联系人列表和服务的注册用户之间运行 PSI 协议来以保护隐私的方式完成。后一种方法被 Signal 和 Secret 应用程序使用，但由于性能原因，它们使用了不安全的朴素散列 PSI 协议。由于可扩展性的原因，Signal 计划使用基于英特尔 SGX 的解决方案，如 Tamrakar 等人（2017）提出的。

在这些情况下，每个用户有少量的记录，例如，，而服务有数百万的注册用户（在我们的实验中，我们使用）。因此可以认为，。在我们最好的 PSI 协议中，客户端只需要内存，对称加密操作，和廉价哈希表查询，而通信是。(通信开销确实很高，因为它取决于，但如果要防止蛮力搜索，这似乎是不可避免的）。

1.2 PSI 协议的分类

安全地将两个集合相交而不泄露任何信息（除了相交的结果）是安全计算中最突出的问题之一。已经提出了几种实现 PSI 功能的技术，如高效但不安全的朴素散列解决方案，需要半信任的第三方的协议，或两方 PSI 协议。最早提出的两方 PSI 协议是基于公钥密码学的特殊用途解决方案。后来，人们提出了使用基于电路的安全计算通用技术的解决方案，这些技术大多基于对称密码学。最近的发展是仅基于 OT 的 PSI 协议，并结合了对称加密基元的效率和特殊目的优化。PSI 协议已经在智能手机上实现和评估（Huang 等人，2011；Asokanetal.2013；Kissetal.2017）。

一个朴素的解决方案：当遇到 PSI 问题时，大多数新手都会想出一个解决方案，即双方都对他们的输入应用一个加密哈希函数，并比较这些哈希值。虽然这个协议非常有效，但如果输入域很小或熵很低，它就不安全，因为一方可以很容易地进行蛮力攻击，将哈希函数应用于可能出现在输入集中的所有项目，并将结果与收到的哈希值进行比较。(当 PSI 的输入具有高熵时，可以使用比较输入的哈希值的协议（Nagy 等人，2013））。

基于第三方的 PSI：已经提出了几个利用额外方的 PSI 协议，例如，Baldwin 和 Gramlich（1985）。在 Hazay 和 Lindell（2008）中，一个可信的硬件令牌被用来评估一个不经意伪随机函数（OPRF）。在 Fischlin 等人（2011）中，这种方法被扩展到多个不可信的硬件令牌。Kamara 等人（2014）提出了几个高效的 PSI 服务器辅助协议，这些协议使用一个不持有输入、不接收输出的第三方，并假定其不与任何一方合作，并进行了基准测试。外包 PSI 协议，如 Abadi 等人（2015，2017）和 Oksuz 等人（2017），允许重复使用外包给云的加密数据集，但在单次运行中的效率低于 Kamara 等人（2014）。

基于公钥的 PSI：Meadows（1986）提出了一个基于 Diffie-Hellman（DH）密钥协议的 PSI 协议（Shamir（1980）和 Huberman 等人（1999）提出了相关想法）。他们的协议是基于 DH 函数的换元特性，并被用于私人偏好匹配，这使得双方可以验证他们的偏好是否在某种程度上匹配。

Freedman 等人（2004）在标准模型（而不是在基于 DH 的协议中假设的随机预言机模型（ROM））中引入了对半诚实的和恶意的对手安全的 PSI 协议。该协议基于多项式插值，并在 Freedman 等人（2016）中进行了扩展，提出了对恶意对手具有基于模拟安全性的协议，并评估了所提散列方案的实际效率。我们在第 3 节讨论所提出的散列方案。Freedman 等人（2005）提出了一种类似的方法，使用 OPRF 来执行 PSI。Kissner 和 Song (2005) 提出了一个使用多项式插值和微分来寻找多集之间的交叉点的协议。

Cristofaro 和 Tsudik (2010) 提出了另一个 PSI 协议，该协议使用公钥加密技术（更具体地说，盲化 RSA 操作），并以元素的数量进行线性扩展。在 Debnath 和 Dutta（2015）中，介绍了一个基于布隆过滤器的 PSI 协议系列，实现了 PSI、PSI 卡度和认证的 PSI 功能。这些协议也使用公钥操作，与元素的数量成线性关系。

基于电路的 PSI：通用的安全计算协议在过去十年中得到了很大的效率改进。它们允许对任意函数进行安全评估，表示为算术或布尔电路。Huang 等人（2012）提出了几个用于 PSI 的布尔电路，并使用姚氏混淆电路进行了评估。作者表明，他们的 Java 实现随着安全参数的增加而扩展得非常好，并且在更大的安全参数下优于 Cristofaro 和 Tsudik（2010）的盲化 RSA 协议。我们在第 4 节中对基于电路的 PSI 进行了思考并提出了新的优化方案。

基于 OT 的 PSI：Dong 等人（2013）给出了一个基于 OT 扩展的布隆过滤器的 PSI 协议，实现了对半诚实和恶意对手的安全性，Pinkas 等人（2014）对半诚实对手进行了优化。最近在 Lambæk（2016）和 Rindal 和 Rosulek（2017a）中，表明基于布隆过滤器的协议对于恶意对手来说是不安全的。Rindal 和 Rosulek（2017a）的作者展示了如何修复基于布隆过滤器的恶意安全协议，并给出了第一个恶意安全 PSI 协议的实现，该协议在 200 秒内计算出两个各有一百万个元素的集合的交集。

在 Rindal 和 Rosulek（2016）中，我们 Pinkas 等人（2014）的基于 OT 的 PSI 协议被扩展到针对弱恶意对手的安全性，并被用作批量双执行姚氏混淆电路协议的构建块。在 Lambæk（2016）中，我们 Pinkas 等人（2015）的基于 OT 的 PSI 协议对半诚实的和恶意的是安全的。Kolesnikov 等人（2016）给出了我们在 Pinkas 等人（2015）的基于 OT 的 PSI 协议的改进版本，该版本使用 Kolesnikov 和 Kumaresan（2013）的 OT 扩展协议（参见第 2.2.3 节）提出了一个 OPRF 的有效构造。作者的主要观点是，Kolesnikov 和 Kumaresan（2013）的 OT 扩展不需要纠错码，而是可以使用伪随机码，它可以由伪随机发生器生成。然后，作者将他们高效的 OPRF 构造应用于我们的 Pinkas 等人（2015）协议，大大减少了 OT 中的通信量，这相当于代码长度。特别是，作者表明，他们的构造实现了独立于元素的比特长度的性能。Kolesnikov 等人（2016）的 OPRF 构造与我们在第 5 节中描述的新 OPRF 构造类似。这两项工作的想法是使用更大的代码实例化隐含在 Pinkas 等人（2015）基于 OT 的 PSI 协议中的 OPRF。然而，虽然 Kolesnikov 等人（2016）用伪随机码取代了纠错码，但我们保留了纠错码，但使用较小的、定制的代码。我们使用 Schürer 和 Schmid（2006）的代码表与 Kolesnikov 等人（2016）的伪随机代码大小比较了的小值的代码大小，见表 1。虽然我们的实例化对于小的值需要较少的通信，但它并没有实现独立于的性能，而且生成这样一个小的定制代码是一个非难的问题。在本文的其余部分，我们固定了一个位长为的纠错码，它支持 PSI 目前所有的实际应用，与 Kolesnikov 等人（2016）相比，它使完整的 PSI 协议的通信开销系数为 1.10 倍到 1.15 倍。总的来说，我们认为我们的工作是对 Kolesnikov 等人（2016）工作的补充，人们可以根据参数对底层代码进行实例化，以实现最佳的整体性能。事实上，在另一项独立和平行的工作中（Orrù 等人，2017），我们对底层代码进行实例化的方法能够使 PSI 协议扩展到恶意接收者，这对 Kolesnikov 等人（2016）的实例化方法不起作用。最后，请注意，Kolesnikov 等人（2016）和 Orrù 等人（2017）的工作也得益于我们第 3 节改进的散列分析。

表 1. 在不同的值下，基础代码的比特长度（相当于每 OT 的通信量）。

1.3 我们的贡献

我们调查了现有的针对半诚实对手的安全 PSI 协议和带有可信第三方的解决方案。然后，我们详细描述了半诚实安全的 PSI 协议，并利用仔细分析的 OT 扩展的特点改进了一些协议的性能。我们介绍了一个新的基于 OT 的 PSI 协议，对最有前途的半诚实安全 PSI 协议进行了详细的实验比较，并评估了它们与目前在现实世界应用中使用的不安全的朴素散列协议相比的开销。我们的贡献如下：

哈希的具体参数估计：Freedman 等人 (2004) 在 PSI 的背景下建议使用散列到桶的方法来减少配对比较的开销。然而，他们对相关参数的分析只是渐进式的。在第 3 节中，我们对 Freedman 等人（2004）提出的散列到桶的技术进行了经验分析，并确定了这些方案的具体参数。此外，在第 3.3 节中，我们利用 Arbitman 等人（2010）的基于排列组合的散列技术来减少存储在桶中的表示的比特长度。这提高了 PSI 协议的性能，这些协议需要的开销与元素的比特长度成线性关系，例如第 4.2 节和第 5 节的协议。

对现有协议的优化：我们利用最近对 OT 扩展的优化改进了电路协议（Asharov 等人，2013）。特别是，在第 4 节中，我们评估了 Huang 等人（2012）对 GMW 协议的安全评估的基于电路的解决方案，并利用随机 OT 的特点（参见第 2.2 节）来优化多路复用器门的性能（该门构成了大约三分之二的电路）。此外，在第 4.2 节中，我们概述了如何使用基于排列组合的散列技术来进一步提高基于电路的 PSI 的性能。

一种新的基于 OT 的 PSI 协议：我们提出了一个新的基于 OT 的 PSI 协议（第 5 节），并直接受益于高效 OT 扩展的改进（Kolesnikov 和 Kumaresan 2013; Asharov 等人 2013）。我们的 PSI 协议使用一个高效的 OPRF，它是基于 Kolesnikov 和 Kumaresan（2013）的选的 OT 扩展协议实例化的，并使用第 3 节的散列技术将通信开销从减少到。由此产生的协议具有非常低的计算复杂度，因为它主要需要对称密钥操作，甚至比之前一些基于公钥的 PSI 协议的通信量还要少。

PSI 协议的详细比较：我们使用最先进的加密技术实现最有前途的 PSI 协议，并在一个平台上比较它们的性能。我们的实现可以在 http://encrypto.de/code/JournalPSI，作为开放源代码。据我们所知，这是第一次进行如此广泛的比较，因为以前的比较要么是理论上的，要么是比较不同平台或编程语言上的实现，要么是使用没有最先进优化的实现。我们的实现和实验将在第 6 节详细描述。某些实验结果是出乎意料的。我们在表 2 中对我们的结果做了部分总结。接下来我们简要介绍一下我们最突出的发现。

基于 DH 的协议（Meadows 1986）是第一个 PSI 协议，实际上是最有效的通信方式（当使用椭圆曲线加密实现时）。因此，它适用于有强大计算能力但连接能力有限的远方当事人的情况。
基于电路的通用协议（Huang 等人，2012）的效率低于较新的基于 OT 的构造，但它们更灵活，可以很容易地适应计算集合相交功能的变体（例如，计算相交的大小是否超过一些阈值）。我们的实验也支持 Huang 等人（2012）的说法，即基于电路的 PSI 协议比 Cristofaro 和 Tsudik（2010）的基于盲化 RSA 的 PSI 协议在较大的安全参数和足够的带宽下更快。
与不安全的朴素散列解决方案相比，以前的 PSI 协议在运行时间或通信方面的效率至少低两个数量级。我们的基于 OT 的 PSI 协议在运行时间和通信方面都将这种开销降低到只有一个数量级。
当与大小不等的集合相交时（），大多数协议之间的运行时间差异仍然与集合大小相等（）的运行时间差异相似。唯一的例外是新增加的基于电路的 OPRF 协议（第 4.3 节），它在不等的集合大小上实现了与朴素散列和服务器辅助解决方案类似的性能。

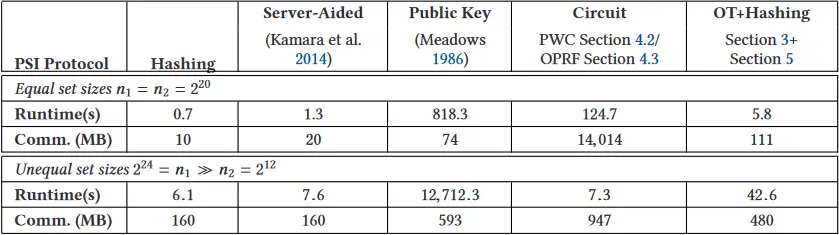
表 2. 单线程在千兆位局域网上对具有个元素和位安全的集合的隐私集合求交集协议的运行时间和传输的数据

1.4 对会议版本的补充

本文是会议论文（Pinkas 等人 2014）和 Pinkas 等人（2015）的显著扩展和改进版本。与这些论文相比，我们增加了以下贡献：

更广泛的范围：我们扩大了工作范围，在第 4.3 节中对 Pinkas 等人（2009）的基于电路的 OPRF 协议进行了描述和基准测试。

扩展的哈希参数分析：我们为使用成对比较的方案扩展了散列参数分析。在我们以前的工作中，我们只对一个特定的参数集的散列失败进行了约束，该参数集是为一个用例定制的。然而，PSI 协议表现良好的散列参数会随着设置的不同而改变（不平等的集合大小，不同的网络，等等）。我们展示了不同参数之间的权衡，从而产生了一大批在不同设置下表现良好的参数。

优化：在以前的工作中，我们基于 OT 的 PSI 协议在输入的比特长度上进行了线性扩展，这降低了它在任意输入数据上的性能。现在，我们在第 5 节中概述了如何通过使用底层基元的更有效实例来实现独立于比特长度的性能（参见第 2.2.3 节）。

不等值集的大小：我们将工作的重点扩展到不等值集的大小，其中 . 这种设置与使用情况有关，例如，终端用户想将其数据（几百个元素）与公司的数据库（几百万个元素）进行比较。我们展示了如何修改基于电路的协议（第 4.3 节）以及我们基于 OT 的协议（第 3.2.2 节）以有效地扩展到这种设置，并对协议进行了实验（第 6.2.3 节）。

可扩展性：到目前为止，对安全的两方 PSI 协议进行评估的最大集合的大小为（Pinkas 等人，2015）。我们通过处理两个各由 10 亿元素组成的集合来证明我们新的基于 OT 的 PSI 协议的可扩展性（第 6.2.4 节）。

2 初步了解

我们在第 2.1 节中给出了我们的符号和安全定义，在第 2.2 节中回顾了最近关于 OT 的相关工作，并在第 2.3 节中概述了如何将大的输入散列到小的域中。

2.1 符号和安全定义

我们把双方称为和，他们各自的输入集称为和，，。我们把中的元素称为，把中的元素称为，每个元素都有位长（关于和的关系，请参考第 2.3 节）。我们用表示一个列表中的第个元素，用表示两个等长的比特串之间的比特与，用表示比特异或。我们用（或）来表示一串恒定的个（或）。我们使用一个相关稳健函数（CRF）（参见第 2.1 节），一个伪随机发生器（PRG），一个伪随机置换（PRP），和一个 OPRF（见下面的定义）。我们用表示在位字符串上的个并行的选的 OT，用表示。以类似的方式，我们表示随机 OT 功能（参见第 2.2.2 节），其中选择个随机位字符串的元组的功能为。我们根据 NIST 指南（NIST 2012）将密钥大小固定为位安全级别：对称安全参数，非对称安全参数，统计安全参数，使用点压缩时 Koblitz 曲线的椭圆曲线大小（这是一个坐标和一个符号位的比特数）。我们表示并固定影响某些协议正确性的散列失败参数为，意味着散列失败发生的概率小于。

对手的定义：安全计算文献考虑了两种具有不同强度的对手：半诚实的对手试图从给定的协议执行中尽可能多地了解信息，但不能偏离协议步骤。半诚实的对手模型适合于这样的场景：通过软件证明保证预定软件的执行，或者不受信任的第三方能够在协议执行后获得协议的记录，无论是通过偷窃还是通过法律强制披露。更强大的恶意对手通过能够任意地偏离协议而扩展了半诚实的对手。

大多数 PSI 的协议，以及这篇文章，都侧重于针对半诚实对手的安全解决方案。恶意设置的 PSI 协议是存在的，但它们的效率不如半诚实设置的协议（例如，见 Freedman 等人（2004），Cristofaro 等人（2010），以及 Rindal 和 Rosulek（2016，2017a，2017b））。目前，最快的恶意安全协议（Rindal 和 Rosulek 2017b）只比 Kolesnikov 等人（2016）的半诚实协议慢 3 倍。我们还注意到，用姚氏协议评估的基于电路的 PSI 协议可以通过使用具有恶意安全的 OT 扩展来有效地防止恶意客户端（例如 Asharov 等人（2015）），这增加了很少的开销：基于 OPRF 的协议直接和基于 SCS 的协议需要我们添加一个小电路，确保输入被排序。

安全定义：按照 Goldreich（2004）的定义，如果参与协议的一方所能计算的东西只能根据这一方的输入和输出来计算，那么这个协议就是安全的。也就是说，在协议中传递的实际信息除了输入和输出之外，没有提供其他的信息。这个定义是基于模拟范式而正式确定的：要求在协议执行中一方的观点（即该方在协议中发送和接收的所有消息）可以仅根据其输入和输出进行模拟。我们注意到，在半诚实对手的情况下，以及协议计算确定性功能（如交集功能）的情况下，只需模拟器输出被对手控制的一方的观点即可。关于安全的详细定义，见 Goldreich（2004）。

随机预言机模型 (ROM)：和以前大多数关于高效 PSI 的工作一样，我们使用 ROM 来实现更高效的实现（Bellare and Rogaway 1993）。加密结构的安全性可以在 "标准模型" 中得到证明，在该模型中，安全性是基于经过充分研究的复杂性假设，或者在 ROM 中，它是基于将散列函数建模为随机函数（Bellare 和 Rogaway 1993）。关于 ROM 有很多批评意见，在密码学证明理论中，这种模型被认为是启发式的。然而，ROM 中的协议往往比在标准模型中证明的协议更有效。

使用 ROM 的效率提升在 PSI 的协议方面尤其如此。我们描述的唯一一个在标准模型中的半诚实协议是 Freedman 等人（2004，2016）的基于不经意多项式评估的协议，但该协议的效率低于我们介绍的其他协议。基于公钥的协议（基于 DH 和盲化 RSA）使用一个哈希函数，该函数必须被建模为随机预言机，或者使用另一个非标准假设进行建模。其他协议（通用协议，以及基于布隆过滤器的协议和新的基于 OT 的协议）可以在没有随机预言机假设的情况下实现，但是为了加快这些协议中 OT 的计算，我们必须使用随机 OT 扩展，其有效实现依赖于一个必须被建模为随机预言机的函数。

相关性稳健函数 (CRF)：一个 CRF 是一个函数，对于这个函数，给定均匀和随机选择的，对抗者无法从计算上区分与均匀分布。这是一个比 ROM 更弱的假设，在 OT 扩展以及姚氏混淆电路协议中使用。传统上，许多实现都使用哈希函数（如 SHA）来提高性能。Bellare 等人（2013）提出了姚氏混淆电路协议中的 CRF 实例，该实例使用固定密钥的 AES 并极大地提高了性能，Zahur 等人（2015）对该实例进行了改进，用于半门方案。在本文中，我们使用了这两种优化方法。

不经意伪随机函数：OPRF（Freedman 等人，2005）是一个函数，给定的一个密钥和的一个输入元素，计算并输出到。没有得到任何输出，也没有学到关于的信息，而没有学到关于的信息。OPRF 可以用于 PSI，首先在的集合上评估 OPRF 协议，然后让知道密匙的在自己的集合上本地评估 OPRF，并将 OPRF 的输出发送给，后者计算出一个明文交集。存在几种 OPRF 的实例，在 Freedman 等人（2005）中有所描述：基于通用安全计算技术（使用 AES 电路（Pinkas 等人，2009）），基于 DH，或基于 OT。在第 4.3 节，我们分析了基于通用安全计算的 OPRF 实例的效率。在第 5 节中，我们给出了基于 Kolesnikov 和 Kumaresan（2013）的选的 ROT 协议的更有效的基于 OT 的实例化。

2.2 不经意传输

OT 是安全计算的一个主要构建模块。当在位字符串上执行次选的 OT 调用（记作）时，发送方持有个消息对（ , ），其中，而接收方持有位选择向量。在协议结束时，收到，但对一无所知，而对一无所知。许多 OT 协议已经被提出，最值得注意的是（对于半诚实模型）Naor-Pinkas OT（Naor 和 Pinkas 2001），它使用公钥操作，在执行个 OT 时，其摊销复杂度为个公钥操作。

OT 扩展（Beaver 1996；Ishai 等人 2003）将昂贵的公钥操作数量减少到只有，并使用更有效的对称加密操作来计算协议的其余部分，其速度快了几个数量级。安全参数基本上与 OT 的数量无关，可以小到。因此，执行 OT 的计算复杂性降低到如此程度，以至于网络带宽成为主要瓶颈（Asharov 等人，2013）。

最近，OT 扩展协议的效率得到了广泛的关注。在 Kolesnikov 和 Kumaresan（2013）中，展示了一个高效的选的 OT 扩展协议，该协议对于短信息来说在中具有亚线性的通信。Asharov 等人（2013）和 Kolesnikov 和 Kumaresan（2013）概述了另一项协议改进，它将从到的通信减少了一半。此外，一些工作（Asharov 等人，2013；Nielsen 等人，2012）通过使用 OT 的变体，即随机 OT，提高了 OT 的效率。在随机 OT 中，( , ) 是在 OT 中统一随机选择的，并被输出到，从而去除从到的最终消息。随机 OT 对许多应用都很有用，我们展示了它如何减少 PSI 的开销。接下来我们将详细描述 Asharov 等人（2013）和 Ishai 等人（2003）的 OT 扩展协议、随机 OT 功能，以及 Kolesnikov 和 Kumaresan（2013）的选的 OT 扩展协议。

2.2.1 2 选 1 的 OT 扩展

(Ishai 等人 2003）描述了一个选的 OT 扩展协议，它将（次比特的 OT）扩展到（次比特的 OT）。我们在协议 1 中描述了 Ishai 等人（2003）的 OT 扩展协议和 Asharov 等人（2013）的优化。

的输入：对比特字符串，。
的输入：选择向量。
公共输入：对称安全参数和基础 OT 的数量。
预言机和加密基元：双方都可以访问一个预言机，一个 PRG , 和一个 CRF 。
协议：
1. 初始化一个随机向量，选择个随机密钥对 , 其中。
2. 双方调用预言机，在第个 OT 中，扮演输入为的接收方，扮演输入为的发送方。
3. 计算，，并将发送给 , 对于。令表示一个由生成的随机位矩阵，其中第列是，第行是 , 对于和。
4. 定义，注意。
5. 令表示位矩阵，其中第列是，第行是，注意。
6. 发送，对于每个，其中，
7. 计算 , 对于。
8. 输出：没有输出；输出。

协议 1

效率：总的来说，当使用 OT 扩展时，中的发送方需要评估个 CRF 和个 PRG，并发送个比特，而接收方则需要评估个 CRF 和个 PRG，并发送个比特。(此外，还有一个基于公钥的 OT 的预处理成本，如果，与主协议相比可以忽略不计）。

2.2.2 随机 OT 扩展

为了提高特定环境下 OT 扩展协议的效率，一些工作（Nielsen 等人，2012；Asharov 等人，2013）使用了一种特殊用途的 OT 功能，称为随机 OT。在随机 OT 中，（ , ）是在 OT 过程中统一随机选择的，并被输出到。通过省去从到的最后一条包含的消息，可以得到一个随机 OT 扩展协议。更详细地说，对协议没有输入，并在协议 1 的步骤 6 中设置，而在步骤 7 中设置。然后输出对位字符串，输出。这个随机 OT 扩展协议将必须发送的比特从减少到，代价是更强的假设，即被建模为随机预言机模型（ROM）而不是 CRF。

2.2.3 N 选 1 的 OT 扩展

在 Kolesnikov 和 Kumaresan（2013）中，引入了一个高效的选的 OT 扩展协议，允许以的亚线性通信来传输短信息。该协议建立在 Ishai 等人（2003）的原始 OT 扩展协议的基础上，并使用纠错码对 R 的选择进行编码，该码用位码字对位字进行编码，它们之间至少有的汉明距离。我们在协议 2 中强调了 Kolesnikov 和 Kumaresan（2013）的选的 OT 与 Ishai 等人（2003）选的 OT 的不同。

的输入：个位元组字符串，。
的输入：选择数，。
公共输入：对称安全参数，，纠错码。
协议：
1. 计算 , ，并将发送给，对于和。注意：表示一个随机位矩阵，其中第列是，第行是（对于和也是如此。）。
2. 定义，注意。
3. 对于每个和，计算并发送。
4. 输出：没有输出；输出。

协议 2

在这个选的 OT 扩展协议中，有两件事值得注意。首先，我们也可以通过让设置和设置来使用随机 OT 扩展功能。其次，为了达到与 Ishai 等人（2003）的原始选的 OT 扩展协议中相同的计算安全级别，各方必须将基础 OT 的数量增加到底层代码的码字长度，这取决于（参见 Kolesnikov 和 Kumaresan (2013)）。增加基础 OT 的原因是，码字之间的汉明距离必须至少是。对于，Kolesnikov 和 Kumaresan（2013）提议使用 Walsh-Hadamard 码，它将多达个字编码为长度为的码字，相对汉明距离为。然而，在我们基于 OT 的 PSI 协议中，我们使用位元素作为 Kolesnikov 和 Kumaresan（2013）的选的 OT 协议的输入，因此需要处理。为了处理这样一个位元素，我们需要找到一个纠错码，以相对汉明距离位的码字和短码尺寸处理输入元素。作为一个例子，当处理位的元素时，我们可以使用大小为位的代码，如 Schürer 和 Schmid（2006）中给出的。

在文章的其余部分，为了便于表述，我们固定了一个线性 BCH 码，产生于 Morelos-Zaragoza（2006），它将多达个字编码为长度为的码字，相对汉明距离为，这被表示为一个码。使用第 3.3 节中概述的基于排列组合的散列技术，并假设比特的统计安全性，这使我们能够处理具有多达 1000 亿（）个元素的集合，而不依赖于其比特长度，这对大多数应用来说已经足够了。

效率：使用 Kolesnikov 和 Kumaresan（2013）的选的 OT 扩展协议和我们的线性 BCH 码评估一个选的 ROT 需要比特的通信和个 CRF 评估。请注意，尽管选的 OT 的 CRF 评估的高数量对于大来说似乎令人望而却步，但在我们的协议中，我们只需要执行恒定数量（例如）的 CRF 评估。相比之下，从选的 OT 扩展中朴素地建立选的 ROT 需要的选的 OT 调用，因此需要比特的通信和的 CRF 评估。更具体地说，当使用第 5 节中我们基于 OT 的 PSI 协议计算两个百万元素集的交集时，我们会有，因此使用 Kolesnikov 和 Kumaresan（2013）的选的 OT 扩展协议需要位通信，使用 Ishai 等人（2003）的常规选的 OT 扩展协议以及 Asharov 等人（2013）和 Kolesnikov 和 Kumaresan（2013）最新的优化，需要位通信。

2.3 将输入哈希到较小的域

一些 PSI 协议的性能取决于其输入的表示长度。对于为输入表示的每一个比特运行一个 OT 的协议来说尤其如此，例如第 4.2 节和第 5 节中描述的协议。

当原始输入表示是稀疏的，我们可以首先使用哈希函数将输入项目的身份映射到具有较短表示的较小域中的身份。然后我们在该表示上运行原始协议，从而使执行效率更高。新域的大小应该足够大，以便没有两个不同的输入项目被映射到相同的值。与生日悖论有关的这种映射的理论分析表明，当使用随机哈希函数将个项目映射到大小为的域时，遇到碰撞的概率为，并且可以近似为（见 Motwani 和 Raghavan（1995，45）。让我们把中项目的表示长度表示为。那么，因此

3 散列方案和 PSI

计算两个集合之间的明文交集通常是使用散列技术完成的。双方商定一个公开的随机散列函数，将元素映射到一个由多个桶组成的散列表。如果一个输入元素在交集中，双方都会把它映射到同一个桶。因此，双方只需要比较在同一桶中的元素，以确定相交的元素。因此，对于成对的比较，元素之间的平均比较次数可以从减少到。

以类似的方式，隐私计算值之间平等性的 PSI 协议可以使用散列技术来减少比较的数量（Freedman 等人，2004，2016）。这种隐私平等性测试协议的例子有 Freedman 等人（2004）、Huang 等人（2012）和 Carter 等人（2013），第 4.2 节的基于电路的协议或第 5 节的基于 OT 的协议。当朴素地使用散列技术时，如果 n 个项目被映射到个桶，那么一个桶中的平均项目数是，检查一个桶中的交叉点需要的工作，因此比较的总数是。然而，隐私性要求双方互相隐藏他们的输入有多少被映射到每个桶。因此，我们必须事先计算出将被映射到最多的桶中的项目数量（概率很高），然后将所有桶设置为该大小。(这可以通过在没有完全被占用的桶中存储虚拟物品来实现。) 这种变化隐藏了桶的大小，但也增加了协议的开销，因为每个桶的比较次数现在取决于最多桶的大小（最坏的情况），而不是桶内的实际项目数（平均情况）。

事实上，这种最坏情况分析是平衡安全和效率的关键。一方面，如果估计过于乐观，一方未能执行映射的概率就变得不可容忍。结果，输出可能是不准确的（因为不是所有的项目都能被映射到桶），或者一方需要请求一个新的散列函数（这个请求会泄露该方输入集的信息）。另一方面，如果分析过于悲观，所进行的比较的数量和因此而产生的协议开销会变得非常大。Freedman 等人（2004，2016）的工作为这种分析和由此产生的开销给出了渐进值。他们把为散列方案设置适当参数的任务留给了未来的工作。

在本节中，我们重新审视 Freedman 等人（2004，2016）使用的简单散列（第 3.1 节）和布谷鸟散列（第 3.2 节）方案。我们描述了如何在 PSI 的背景下使用这两种散列方案，并给出了一个具体的参数分析，以平衡安全性和效率。最后，我们展示了如何使用基于包络的映射来减少存储在桶中的表征的比特长度，这提高了一些 PSI 协议的性能（第 3.3 节）。

请注意，对于我们的散列失败分析，我们使用一个专门的散列失败参数，这与统计安全参数不同。我们使用一个专门的参数，因为我们的分析需要运行实验来确定具体数字，这将花费几十万美元在亚马逊 EC2 云中进行次反复。因此，我们进行了实验，给出了的具体数字，并从这些结果中插值到。

3.1 简单哈希

在最简单的散列方案中，散列表由个桶组成。散列是通过使用散列函数将每个输入元素映射到一个桶来完成的，该函数是均匀地随机选择的，与输入元素无关。一个元素总是被添加到它被映射到的桶中，不管其他元素是否已经存储在该桶中。

3.1.1 用于 PSI 的简单哈希

为了在 PSI 的背景下应用简单散列，双方都将他们的元素映射到个桶中。然后，通过让双方分别比较映射到桶的项目来计算交集。为了隐藏映射到一个桶的元素数量，双方需要使用假元素来填充他们的桶，以包含最大个元素。这个最大桶的大小必须确保，除了概率小于，没有一个桶会包含超过的实数元素。

3.1.2 简单哈希参数分析

对的估计已经有了广泛的研究（Gonnet 1981；Raab 和 Steger 1998；Mitzenmacher 2001）。当把个元素哈希到个桶时，Gonnet（1981）表明的概率很大。在这种情况下，映射到一个桶的元素的预期数量和最大数量之间存在差异，它们分别为和。让我们重温一下 Motwani 和 Raghavan（1995）的分析，该分析分析了以下事件的概率，" 个球被随机映射到个桶中，而最多的桶至少有个球 "。

当时：使用位浮点精度的 GMP，我们用公式（3）计算当把元素映射到个桶时的，选择把故障概率降低到和以下的的最小值，并在表 3 中描述了结果。

表 3. 根据公式 (3)，将个项目映射到个桶时，为确保不发生溢出所需的最大桶尺寸

当时：在某些设置中，服务器有一个比客户端大得多的集合。在文章的后面，我们对这种情况进行了实验（参见第 6.2.3 节），有一个大小为的集合，而有一个大小为的集合，两者都将个元素映射到个桶中。为了确定这种情况下的，我们用这些集合的大小评估方程（3），并在表 4 中描述了散列失败概率和的。从结果中，我们可以观察到，随着分数的增长，最大桶数越来越接近预期桶数。

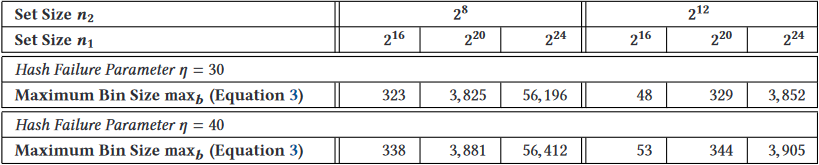
表 4. 根据公式 (3)，将个项目映射到个桶时，为确保不发生溢出所需的最大桶尺寸

3.2 布谷鸟哈希

布谷鸟散列 (Pagh and Rodler 2001) 使用个散列函数将个元素映射到个桶。该方案通过在发现碰撞时重新定位元素来避免碰撞，具体过程如下。一个元素被插入到一个桶。的任何先前的内容被驱逐到一个新的桶，用来确定新的桶的位置，其中当。该程序重复进行，直到没有必要再进行驱逐，或直到进行了阈值数量的重新定位。在后一种情况下，最后一个元素被放入一个特殊的储藏桶。这个方案中的查找是非常有效的，因为它只将与 B 中的个项目和储藏桶中的个项目相比较。散列表的大小取决于散列函数的数量以及储藏桶的大小。选得越大，插入过程成功的可能性就越大，因此桶的数量就越小。另一方面，选择的越大，可以容忍的插入失败就越多。

3.2.1 用于 PSI 的布谷鸟哈希

在使用布谷鸟散列法进行 PSI 时，会出现一个主要问题：每个项目都可以被映射到个桶中的一个，因此不清楚应该用哪个桶来比较自己的输入元素。此外，协议必须向每一方隐瞒另一方为存储一个元素所做的桶的选择，因为这种选择取决于其他输入元素，并可能暴露关于它们的信息。解决这个问题的方法是，使用布谷鸟散列，而则使用个散列函数中的每一个简单散列来映射其每个元素。此外，对于布谷鸟散列，我们必须确保散列成功，但概率小于，因为一方的散列错误会暴露其集合的信息或导致错误的结果。如同在简单散列的 PSI 中（参见第 3.1 节），需要使用假元素将其的桶填充到大小。

3.2.2 布谷鸟哈希参数分析

布谷鸟散列有三个影响散列失败概率的参数：储藏桶大小，散列函数的数量，以及桶的数量（Kirsch 等人，2009）。Kirsch 等人（2009）表明，在常数和的情况下，将个元素散列到个桶中，其中，任何和的情况下，失败的概率为。大 " " 符号中的常数是不明确的，这使得我们很难在一组参数下计算出具体的失败概率。

在下文中，我们根据经验来确定给定的存储空间大小、哈希函数的数量和桶的数量的失败概率。我们分别分析所有三个参数的影响。我们首先固定，散列函数的数量（正如 Kirsch 等人（2009）所做的那样），并确定必要的储藏桶的大小。为了提高性能，我们增加散列函数的数量，并确定不需要储藏的的数量（即）。虽然这两种方法在时都取得了良好的开销，但当双方的集合大小不相等时，它们的表现就很差。因此，在最后一步，我们展示了如何通过增加桶的数量来获得低值的储藏桶大小和低数量的哈希函数的数量，这导致了对不平等集合大小应用的权衡集合。

调整储藏桶大小：在下文中，我们确定确切的储藏桶大小，以确保散列失败概率小于给定的。为了得到具体的数字，我们运行了次布谷鸟散列，其中我们将个项目映射到个桶，对于，使用个散列函数，并记录布谷鸟散列成功所需的储藏桶大小。我们固定，就像在最初的布谷鸟散列与储藏桶的论文中一样（Kirsch 等人，2009）。图 1 中的实线描述了一个大小为的储藏桶防止散列失败的概率。

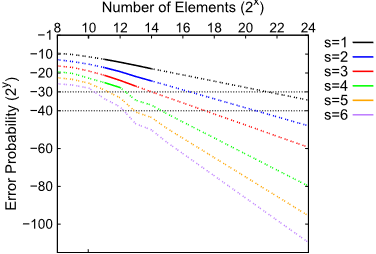
图 1. 在储藏桶大小的情况下，使用布谷鸟散列法与散列函数将个元素映射到个桶的错误概率。实线对应的是实际测量值，虚线是用线性回归法推算的。

从结果中我们可以观察到，为了达到的布谷鸟散列失败概率，我们需要当时，时，和或时的储藏库大小。然而，在我们的实验中，我们需要更小以及更大的值的存储空间，以达到的布谷鸟散列失败概率。为了获得更大的值的失败概率，我们用线性回归法推断结果，并在图 1 中用虚线说明结果。我们在表 5 中给出了在的情况下实现和的散列失败概率的推断的存储空间大小。我们观察到，对于较高的值，实现的失败概率的存储空间大小急剧减少：对于，我们需要一个大小为的存储空间，对于，我们需要，对于我们需要。这一观察结果与渐进的失败概率是一致的。

表 5. 当把个元素映射到个桶中时，达到的故障概率所需的贮藏尺寸

调整哈希函数的数量：最初的布谷鸟散列程序（Pagh 和 Rodler 2004）固定了散列函数的数量。后来在 Dietzfel 桶 ger 等人（2010）中显示，增加散列函数的数量可以实现散列表中桶的更好利用，也就是说，虽然的散列函数的平均利用率约为，但的利用率增加到，为，而为。因此，更高的值使我们能够大幅度地减少桶的数量。然而，与之前的储藏桶分配类似，Dietzfel 桶 ger 等人（2010）的分析只是渐进式的，不允许我们计算具体的散列失败概率。

为了确定具体的失败概率，我们再次使用哈希函数对个元素进行次布谷鸟散列迭代。我们在这个分析中的目标是确定最小数量的桶，在这个过程中，除了概率为的情况下，散列程序没有藏匿成功。为了确定的值，我们在初始化值的基础上运行布谷鸟散列，并在每次发生多于一次的散列失败时将增加。在使用多个哈希函数的实验中，我们发现一个有趣的现象：在某个阈值之后，哈希失败的概率急剧下降，例如。总的来说，我们确定了以下能使散列失败概率小于的桶大小：的，的，以及的。我们通过在的值的基础上增加一个额外的安全系数来推断的值，结果是的，的，以及的。

增加哈希函数数量的后果是，使用简单哈希的一方需要增加最大桶大小。这是由两个因素造成的：一方面，需要将每个元素映射次到它的哈希表。另一方面，由于的减少，各方减少了桶的数量。我们使用方程 3 重新计算了的最大桶大小，并在表 6 中给出结果。鉴于这些结果，我们可以通过将桶的数量与相乘来计算比较的总数。从这些结果中，我们观察到在集合大小相等的情况下实现了最佳性能。

表 6. 根据公式 (3)，当使用个哈希函数将个项目映射到个桶时，为确保不发生溢出而需要的最大桶尺寸

调整桶的数量：个桶和个哈希函数所需的存储空间大小对于小的集合大小（例如，对于）是相对较大的。在集合大小的情况下，这对协议的性能影响不大。然而，在集合大小的情况下，大的存储空间将大大降低性能，因为存储空间中的每个元素都需要与可能有数百万个元素的大集合中的每个项目进行比较。此外，即使增加哈希函数的数量来移除储藏桶，也需要将其百万个元素中的每一个映射到其哈希表中次，这就增加了，从而产生了很大的开销。

为了提高不等量集合的性能，我们固定储藏桶大小和哈希函数的数量，并尝试确定的数量，使散列失败的概率小于。与之前的实验类似，我们运行了次布谷鸟散列，将个项目映射到个桶，，，并记录了布谷鸟散列成功所需的存储空间大小。我们选择，因为它是用户地址簿中联系人数量的一个很好的近似值，并且它被用于我们在第 6.2.3 节的实验。

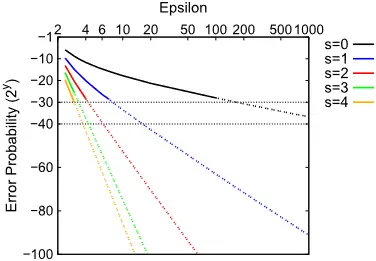
我们的实验结果在图 2 中以实线描述。从结果中，我们可以观察到，随着的增长，需要一个大小的存储空间的概率呈对数下降：虽然对于小的来说，概率下降很快，但对于大的来说，概率下降较慢，例如，当把从增加到时，一个大小为的存储空间的散列失败概率从下降到。另一方面，如果将从增加到，的散列失败概率只从下降到。由于我们感兴趣的是确定，使需要大小为的储藏桶的概率下降到以下，我们通过对数函数使用回归来推断概率。这些估计的概率在图 2 中被描述为虚线，表 7 给出了散列失败概率下降到和以下的最小的。

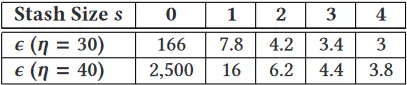
图 2. 在储藏桶大小的情况下，使用布谷鸟散列法和的散列函数将个元素映射到个桶的错误概率。实线对应的是实际测量值，虚线是用对数回归法推算出来的。

表 7. 在固定的储藏桶大小的情况下，哈希失败概率小于所需的桶的数量

估算结果表明，如果将储藏桶大小减少到，我们需要设置来保证的散列失败概率，并设置来保证的散列失败概率。当允许更大的存储量时，急剧下降，允许我们为的散列失败概率设置，为散列失败概率设置。在我们的实验中，和的确切选择取决于集合大小和之间的差异以及所使用的协议（参见第 6.2.3 节），也就是说，如果只有几百个，而有几百万个，选择来实现储藏桶大小可能会更有效。

3.3 基于排列组合的哈希算法

第 4 节中我们基于电路的 PSI 协议和第 5 节中基于 OT 的 PSI 协议的开销取决于双方映射到桶的项目的比特长度。存储项目的比特长度可以根据 Arbitman 等人（2010）提出的基于排列组合的散列技术来减少布谷鸟散列的内存使用。该构造是在算法设置中提出的，以提高内存使用率。据我们所知，这是它第一次被用于安全计算或加密背景。

该结构使用类似 Feistel 的结构。让是一个输入项的比特表示，其中，即等于哈希表中一个条目的索引的比特长度。(我们在此假设哈希表中的桶数是的幂，Arbitman 等人 (2010) 已经说明了如何处理一般情况)。让是一个随机函数，其范围是。然后项目 x 被映射到桶。存储在桶中的值是，它的长度比原始项目的长度短对数位。这是一个很大的改进，因为存储数据的长度大大减少了，特别是当不大于对数的时候。至于安全性，由于函数是随机的，一个桶的最大负载是的概率很高。

映射函数的结构保证了如果两个项目，在同一个桶中存储相同的值，那么一定成立：如果这两个项目被映射到同一个桶，那么。如果存储的值相等，因此满足，那么也一定成立，因此。

作为一个具体的例子，假设，表有个桶。那么存储在每个桶中的值只有位，而不是原来方案中的位。还要注意的是，桶位置的计算需要的一个实例化，这可以用一个中等大小的查找表来实现。请注意，当使用多个哈希函数将一个元素映射到一个桶中时，例如，当使用布谷鸟哈希时，哈希函数的索引需要被添加到桶中的表示，以保持唯一性。Lambæk（2016）也指出了这一观察。

4 基于电路的 PSI

与特殊目的的 PSI 协议不同，我们在本节中描述的协议是基于通用的安全计算技术，可以用于计算任意的功能。半诚实模型中两个最突出的通用安全计算协议是 Goldreich-Micali-Wigderson (GMW) 协议 (Goldreich et al.1987) 和姚的混淆电路协议 (Yao 1986)。Schneider 和 Zohner（2013）对这两个协议进行了详细的描述和比较。这两个协议都是通过将一个函数表示为布尔电路来安全地评估它，其中各方评估加密操作并为电路中的每个门进行通信。因此，通用协议的复杂性通常以电路大小来衡量，也就是门的总数量。此外，GMW 协议的复杂性也以电路深度来衡量，即从任何输入到任何输出的门的最高数量，因为 GMW 协议需要为每个门执行交互。在这一节中，我们概述了 Huang 等人（2012）的排序 - 比较 - 洗牌（SCS）电路，这是一个大小为的布尔电路，用于计算 PSI 功能（4.1 节）。然后，我们展示了如何使用第 3 节中描述的散列方法来实现比 SCS 电路更好的复杂度，使用一个朴素的对偶比较电路（第 4.2 节）。最后，我们重新审视了 Pinkas 等人（2009）的方法，其中通用安全计算技术被用来实例化一个 OPRF（参见第 2.1 节），它被用来处理一方的输入元素（第 4.3 节）。

使用通用协议的好处是，协议的功能可以很容易地被扩展，而不必改变协议或由此产生的协议的安全性。例如，可以直接改变 SCS 和 PWC 协议来计算交集的大小，或者一个函数来输出交集是否大于某个阈值，或者计算与交集中的项目相关的值（例如收入）的总和。使用其他 PSI 协议计算这些变体是不容易的。

4.1 用于 PSI 的排序 - 比较 - 洗牌电路 (SCS)

Huang 等人 (2012) 描述的 SCS 电路是一个大小为的 PSI 的布尔电路。(我们这里指的是使用 Waksman permutation 进行洗牌的 SCS 电路）。SCS 电路计算两个集合之间的交集，首先将两个集合排序到一个单一的排序列表中，然后比较所有相邻的元素是否相等，最后对相交的元素进行洗牌，以隐藏任何可能从结果顺序中得到的信息。

对于位长为的输入，SCS 电路的总体规模是个门，这是由个门的排序电路、个门的比较电路和个洗牌电路的总和。值得注意的是，电路中大约的门是由多路复用器造成的。这些多路复用器门可以在 GMW 中使用向量乘法三元组进行有效评估（Demmler 等人，2015），将 GMW 中的成本从个门降低到相当于位多路复用器的个门。

证实了这一点。在第 6 节的实验中，我们使用 GMW 来评估 SCS 电路的深度优化变体，其中比较门有个门，而不是个，但对于位值来说，其深度为，而不是（参见 Schneider 和 Zohner（2013））。因此，SCS 电路的大小从大约增加到，但其深度从减少到。使用 Demmler 等人（2015）的向量乘法三元组优化，深度优化的 SCS 电路的大小再次下降到大约。

4.2 成对比较 (PWC) 和哈希算法

执行 PSI 功能的一个更简单的电路是配对比较（PWC）电路，其中集合中的每个元素都与集合中的每个元素进行比较。使用第 3 节中的散列方法，我们可以大大减少比较的次数，如下所示。

双方都使用一个大小为的表来存储他们的元素。我们的分析（第 3.2.2 节）表明，当相应地设置存储空间大小时，对于合理的输入大小（），设置可将错误概率降低到可以忽略不计（参见第 3.2 节）。
使用布谷鸟散列法与个散列函数和一个储藏库将其输入元素映射到个桶；空桶被填充了一个假元素。
使用简单的散列法将其输入元素映射到个桶中。桶的大小被设置为，这个参数的设置是为了确保没有桶溢出（参见 3.1.2 节）。每个桶中的剩余槽被填充了一个哑元素。第 3.1.2 节中描述的分析显示了是如何计算的，并被设置为一个小于的值。
双方安全地评估一个电路，该电路将被映射到桶的元素与被映射到它的每个元素进行比较。
最后，通过安全地评估计算该功能的电路，检查储藏桶的每个元素是否与的所有输入元素相等。
为了减少分桶中元素的比特长度，以及电路的大小，该协议使用了第 3.3 节中描述的基于排列组合的散列。

效率：让是电路中进行的元素比较的数量，，即对于个桶中的每一个，各方对每个桶进行的比较，以及对储藏库中的每个位置进行的比较。每个元素的长度为位，这是使用基于排列组合的散列法将元素映射到桶中后的缩短长度，即。两个位元素的比较是通过计算元素的位，然后计算深度为的个门的树来完成的。这棵树的最顶端的门是一个门。之后，该电路计算涉及中每一项的所有比较结果的。(注意，最多只有一个比较结果是匹配的，因此该电路可以计算比较结果的，而不是）。总的来说，这个电路由大约个门组成，深度为。

优点：PWC 电路比 SCS 电路有几个优点：

与 SCS 电路中的门的数量相比，它是（参见 Huang 等人（2012），并回顾，以及表 3 中被证明在和时不大于（而且渐进地不大于）。与 SCS 电路中的非线性门的数量相比，PWC 电路的非线性门的数量要小倍以上（尽管两个电路的渐进大小相同）。
PWC 电路的主要优点是的低深度，这也与元素数无关。这影响了 GMW 协议的开销，该协议需要对电路中的每一级进行一轮交互。
PWC 电路的另一个优点是其结构简单。每个桶都要评估相同的小型比较电路。这一特性使得 SIMD（单指令多数据）评估具有很低的内存占用率，并易于并行化。
最后，SCS 电路的效率是为相等的集合大小量身定做的。对于不相等的集合大小，它的电路尺寸不能很好地扩展，最多只能提高倍。相反，PWC 电路对于不相等的集合大小的扩展要好得多，在我们的实验中，它提高了倍到倍。

4.3 对 OPRF 的安全评估

Freedman 等人（2005）和 Pinkas 等人（2009）概述了另一种基于电路的 PSI 方法，并使用 OPRF（参见 2.1 节）。在这个协议中，各方使用安全计算来评估一个伪随机函数，它把的随机密钥和的元素作为输入，并把输出返回给。安全计算的使用保证了不经意性，即没有学到关于或的信息，而没有学到关于的信息。然后，可以通过计算他的 OPRF 的输出与发送的元素之间的明文交集来识别交集。

效率：基于电路的 OPRF 构造的效率主要取决于伪随机函数的实例化。虽然有可能用 Albrecht 等人（2015）等为安全计算而优化的密码来实例化，但我们在效率分析中考虑了基于 AES 的实例化，因为 AES 的安全性已得到更好的证实，而且今天的许多 CPU 都有 AES 的本地指令（AES-NI）。在 AES 电路中，门的数量为个，其乘法深度为（Boyar 和 Peralta 2010）。总的来说，我们必须进行个平行的不经意 AES 评估，结果是总共有个门，深度为。另一方面，可以对他的元素进行明文 AES 评估，只需要发送个长度为位的抗碰撞字符串。因此，由于常数较大，基于 OPRF 的方法在具体效率上不如 SCS 或 PWC 电路，尽管它的规模为，而其他两个电路的规模为。然而，如果双方的集合大小相差很大，即对于，基于 OPRF 的电路的大小会提高倍，这种方法可以比其他基于电路的构造更有效，甚至比所有其他 PSI 协议更有效，因为这个更大的集合中的元素可以以非常低的成本被处理（参考第 6.2.3 节）。

5 基于 OT 的 PSI

在本节中，我们描述了我们新的基于 OT 的 PSI 协议，其早期版本出现在 Pinkas 等人（2014，2015）中。与会议版本相比，我们改进了我们的协议，使其复杂性现在与现实集合大小的位长无关。我们基于 OT 的 PSI 协议的核心是一个高效的 OPRF（参见第 2.1 节）实例化，使用最近的 OT 扩展技术，特别是随机 OT 功能（Nielsen 等人，2012；Asharov 等人，2013）和 Kolesnikov 和 Kumaresan（2013）的选的 OT，它们基本上是用来实现 OPRF 的。我们的协议分为三个步骤：各方将其元素散列到散列表中，使用 OPRF 掩盖其元素，并计算这些被掩盖的元素的明文交集以识别相交的元素。散列步骤使用第 3 节中的方法，将元素散列到桶中。在下文中，我们将更详细地描述 OPRF 的构造（第 5 节）。

散列：在我们基于 OT 的 PSI 协议的第一步中，双方已经将他们的元素映射到散列表和中，其中表中的元素由于基于包络的映射而具有比特长度（参见 3.3 节）。使用了简单的散列法，因此它的散列表有两个维度（在编程语言中的二维数组的意义上），其中第一个维度针对的是分桶，第二个维度针对的是分桶中的元素。使用了布谷鸟散列法，因此它的哈希表只有一个维度，即解决分桶。然后，我们基于 OT 的 PSI 协议为每个桶评估一个理想的 OPRF 功能（参见第 2.1 节），其中输入一个随机密钥，输入位元素，并获得随机输出。OPRF 必须确保没有学到的输入信息，而且除了对应其元素的输出外没有学到任何信息。由于知道秘密的 OPRF 密钥，它可以在其元素上本地评估，得到，当。

计算 OPRF：主要的观察结果是，我们可以使用 OT 来实例化 OPRF 功能。这一步可以使用随机 OT 来实现，因为不需要发送方明确设置传输值。此外，我们可以使用 Kolesnikov 和 Kumaresan（2013）的选的 ROT 协议，其中发送方收到一个密钥，具有输入的接收方收到。具体来说，对于位的输入，我们使用一个选的随机 OT 在位字符串上（），其中扮演没有输入的发送方，接收随机 OPRF 密钥作为输出，而扮演输入的接收方，获得，对于。然后，可以使用随机 OPRF 密钥，它对应于协议 2 的 Kolesnikov 和 Kumaresan (2013) 协议中的和的值，在其输入值上评估 OPRF 输出，因为，其中是纠错码的第个码字，对于和。事实上，Kolesnikov 等人（2016）在我们的工作中也同时使用了这一观察结果，以实现一个基于 OT 的 PSI 协议，该协议与元素比特长度无关。

计算交叉点：在对所有桶的 OPRF 进行评估后，它将所有的 OPRF 输出收集到集，对集的元素进行排序并发送结果。通过检查是否与 V 中的任何元素匹配来识别是否在交集中。如果元素与中的任何元素相匹配，它们的 OPRF 输出将是相等的。如果与中的任何元素都不匹配，它们的 OPRF 输出将不同，但概率为。储藏桶的元素以类似的方式被独立处理：双方都评估 OPRF，获得其储藏桶元素的输出，而对其集合中的每个元素进行本地评估 OPRF，并将混合后的输出发送给，后者识别交集。

效率：主要的计算和通信开销来自于 OPRF 的评估。OPRF 的效率在很大程度上取决于基础实例化。我们使用 Kolesnikov 和 Kumaresan（2013）的协议和 Morelos-Zaragoza（2006）生成的线性 BCH 码来实例化映射位输入到位输出的 OPRF（参见 2.2.3 节）。总的来说，各方进行 OPRF 评估，对应于，其中储藏桶大小和的数量被选择来实现可忽略的布谷鸟散列错误概率（参见 3.2.2 节）。关于通信，为发送比特，而为稀疏的 OPRF 输出发送比特，其中是用于布谷鸟散列的哈希函数的数量（参见第 3.2.2 节）和。关于计算，请注意，在一个朴素的评估中，发送者需要进行个 CRF 评估，每个消息一个。然而，由于只需要获得其分组中实际元素的输出，它只需要进行次 CRF 评估，这与无关。

正确性：在下文中，我们将分析该方案的正确性。我们假设，在协议 3 中，使用简单散列法将每个元素映射次到哈希表，而使用布谷鸟散列法将每个元素映射一次到哈希表。

如果 , 那么和将在他们的哈希表的一个桶中拥有相同的项目（将项目映射到个桶中的一个，而将项目映射到所有个桶）。对于这个桶，得到作为 OPRF 的输出，可以在本地计算， , 而成功识别了相等。

如果，那么的概率是。然而，我们要求的哈希表中元素的所有 OPRF 输出与的哈希表中元素的所有输出不同，这发生的概率为。因此，为了实现概率为的正确性，我们必须将 OT 的比特长度增加到。

安全性：安全性的证明遵循半诚实对手的安全计算的常见安全定义（Goldreich 2004）。我们表明，PSI 协议中和的观点都可以被模拟，只需给他们对协议的输入和输出。我们假设选的 ROT 协议实现了一个理想的选的 ROT 功能。也就是说，在分析中，我们可以用一个可信方来代替这个协议，该可信方从接收方接收一个输入，而没有从发送方接收任何输入，并向发送方输出一个随机密钥，向接收方输出值。

对观点的模拟是显而易见的，因为它在 PSI 协议中学习的唯一信息是随机 OT 中选择的随机密钥，它与的输入无关。因此，的观点可以通过向它发送一个随机值列表来模拟，按照协议中的定义，用它们来加密它的输入，并将结果发送给。

在协议中的观点包括它在选的 ROT 协议中学习到的的加密输出集合，以及发送给它的加密值集合 (以 permuted 顺序)。如果有两个元素和，且，那么就有相应的值，，其中。基于的伪随机性，，中的所有其他值都与随机值不可区分。因此，鉴于协议的输出（即知道它的每个输入是否在交集中），的视图可以被模拟。集合由随机值组成。对于每个，我们将加入，并将额外的随机值加入。这正是在选的 ROT 由受信任方实施时收到的数值分布。

6 评估

在下文中，我们将评估之前所概述的最有希望的 PSI 协议。我们首先讨论了它们的实现特点，并在理论上对它们进行了比较（第 6.1 节）。然后，我们对不同环境下的协议进行了经验性的性能比较（第 6.2 节）。在整个评估过程中，我们将 PSI 协议分为四类，取决于协议是否基于公钥操作、电路、OT 或提供有限的安全性，并将每一类的最佳结果用黑体字标出。

6.1 理论评估

在评估 PSI 协议的实际性能之前，我们讨论了协议的实现特点，如它们是否适合在有几百万元素的集合上进行大规模的 PSI（第 6.1.1 节）或方案的并行化能力（第 6.1.2 节），并给出它们的渐进计算和通信复杂性（第 6.1.3 节）。

6.1.1 适用于大规模的 PSI

尽管几乎没有讨论过，但在实施对大量数据进行操作的加密方案时，内存消耗是一个非常大的问题。因此，许多实现的 PSI 协议很快就超过了主内存，需要更多的工程努力和更仔细的实现，以便在更大的集合上实现 PSI。事实上，即使计算数十亿元素的集合的明文相交也会成为一个繁琐的问题，因为在执行过程中至少有一个集合需要完全存储。在这种情况下，人们可以将数据存储在磁盘上，这在进行任意查找时，性能会大大降低。

有限安全和基于公钥的 PSI：朴素哈希、服务器辅助和基于公钥的 PSI 方案是非常有效的内存，因为它们只在单个元素上操作，并且可以很容易地进行流水线操作，即使在标准 PC 上也可以对数百万个元素进行 PSI。

基于电路的 PSI：基于电路的 PSI 方案有很高的内存消耗。在我们的实现中，如果不再使用门，我们会评估和删除门以减少内存消耗。姚明的混淆电路比 GMW 有更高的内存消耗，因为每条线都要存储比特的密钥，而不是单比特。像 FastGC（Huang 等人，2011；Henecka 和 Schneider，2013）那样的流水线电路生成和评估将使我们能够在更大的集合上执行 PSI。我们的 Yao 和 GMW 实现的主要内存限制来自于电路必须被完全建立并存储在内存中。为了减少电路的内存占用，我们建立了以 SIMD 方式多次并行评估的电路，即在多个值上并行评估电路。这种 SIMD 评估特别有利于 PWC（第 4.2 节）和 OPRF（第 4.3 节）电路，因为同一个电路在所有元素上都是平行评估的。

基于 OT 的 PSI：Dong 等人（2013）和 Pinkas 等人（2014）的混淆布隆过滤器和随机混淆布隆过滤器 PSI 协议需要随机访问布隆过滤器中的位置来识别相交的元素。因此，整个布隆过滤器需要保存在内存中，或者需要外包给磁盘，但这将导致更高的运行时间。混淆布隆过滤器持有个至少为位的条目，对于 100 万个元素的集合，至少需要。我们基于 OT 的 PSI 协议（第 5 节）的主要内存限制是哈希表，特别是布谷鸟哈希表。虽然简单散列的哈希表可以很容易地存储在磁盘上，但布谷鸟哈希表在驱逐元素时需要执行任意的查找。布谷鸟哈希表最多可以容纳个位长度的元素，对于 100 万个元素的集合来说，其长度为，因此比基于布隆过滤器的协议扩展得更好。

6.1.2 计划的可并行性

我们在实证评估中进行的实验只考虑使用单线程执行。然而，如果有更多的计算资源，这些方案可以使用多线程运行，以提高其性能。然而，请注意，许多协议（即除了基于公钥的协议之外的所有协议）的瓶颈很快就从计算转移到了通信，因为使用 AES-NI 可以非常有效地评估对称加密操作。在下文中，我们将讨论这些方案的并行化能力。

有限安全和基于公钥的 PSI：由于各元素的处理是相互独立的，因此朴素哈希、服务器辅助和基于公钥的 PSI 方案很容易被并行化。所有这些方案中并行化的主要瓶颈是在每个协议结束时进行的哈希值的明文交叉。

基于电路的 PSI：基于电路的 PSI 协议根据底层安全计算协议以不同方式进行并行化。GMW 协议使用 OT 扩展来预计算乘法三元组。这一步是主要的计算工作量，可以很好地并行化。然而，GMW 的电路评估需要各方之间的顺序互动，这种互动在电路的深度上是线性的，不能被并行化。另一方面，姚的混淆电路是一个恒定的回合协议。它的并行化能力取决于基础电路结构。可以分成许多相互独立的子电路的电路，如 PWC 和 OPRF 电路，可以很容易和有效地进行并行化，而所有门都相连的电路，如 SCS 电路，需要依赖电路的方法进行并行化。

基于 OT 的 PSI：对于所有基于 OT 的 PSI 协议，它认为底层的 OT 扩展协议可以很好地并行化。可并行化的主要差异是由于用于将元素映射到相应结构中的散列方案。在 Dong 等人（2013）的基于混淆布隆过滤器的 PSI 协议中，必须提前生成混淆布隆过滤器，而这一步并不能很好地并行化。Pinkas 等人（2014）的随机混淆布隆过滤器协议对此进行了改进，其中混淆布隆过滤器是作为 OT 扩展的输出生成的，因此可以完全并行化。在我们的 OT-PSI 协议中，并行化的主要瓶颈是布谷鸟哈希程序。然而，布谷鸟散列可以被预处理，因为不需要对方的输入。

6.1.3 渐进式性能比较

我们在表 8 中描述了拥有大部分工作量的一方的渐进计算复杂度和 PSI 协议的总通信复杂度。计算复杂度表示为对称加密原语评估数（）和非对称加密原语操作数（）。我们假设每个 OT 有 3 个符号（基于布隆过滤器的协议有 2.5 个符号），姚的协议中每个门有 4 个符号，而 GMW 协议中每个门有 6 个符号。

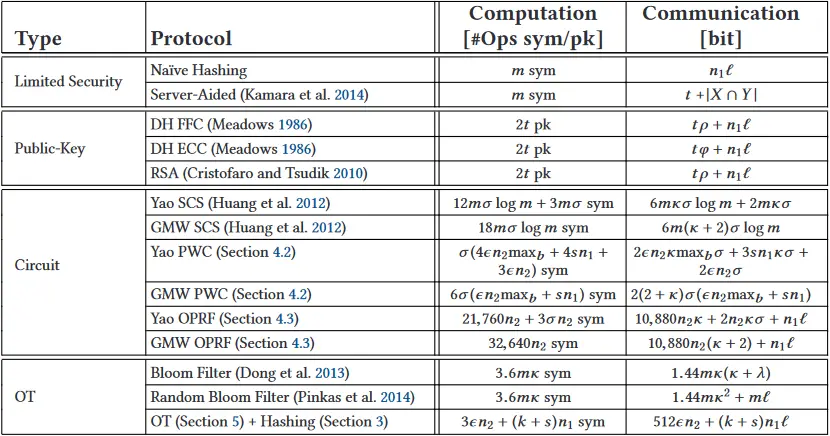
我们从渐进复杂度中得到的最关键的观察是，渐进地，相同类型的方案之间的性能几乎是相等的。朴素散列和服务器辅助协议都需要对每个元素进行次操作，基于公钥的协议都需要对每个元素进行次操作，并需要发送两个密码文本和一个散列值，基于电路的协议都必须执行与电路中的门数量成线性的工作，而基于布隆过滤器的协议都必须执行与布隆过滤器的大小成线性的工作。主要的差异可以在基于 OT 的协议中看到，基于布隆过滤器的协议的通信复杂度随着对称安全参数的变化而呈四次方变化，而我们基于 OT 的 PSI 协议只在安全参数中呈线性变化（我们需要位编码来实现相对汉明距离，参见 2.2.3 节）。

表 8. PSI 协议的渐进复杂度 ( : 集合元素的比特大小； ; ; : 公钥运算； : 对称加密操作； ; , , , : 2.1 节中定义的安全参数； , , , :3.1 节和 3.2 节中定义的哈希参数)。计算给出了需要依次执行的操作的数量。

6.2 实验评估

我们对所提出的半诚实的 PSI 协议的性能进行了实证评估和比较。根据 NIST 的建议，所有协议都以位的安全级别进行实例化（参见第 2.1 节）。我们首先描述了我们的基准测试环境并概述了我们的实现（第 6.2.1 节）。然后，我们在局域网和广域网环境中对协议进行了基准测试，并给出了它们的具体通信情况（第 6.2.2 节）。最后，我们评估了大规模 PSI 的性能（第 6.2.4 节）。

6.2.1 测试环境

我们在一个局域网和一个广域网设置中进行了实验。局域网设置包括两台通过千兆以太网连接的 PC（英特尔 Haswell i7-4770K CPU，3.5GHz，16GB RAM）。广域网设置包括两个亚马逊 EC2 m3.medium 实例（英特尔至强 E5-2670 CPU，2.6GHz，3.75GB 内存），分别位于北弗吉尼亚（美国东海岸）和法兰克福（欧洲），平均带宽为 98MBit/s，平均往返时间为 94ms。

我们在两种情况下评估 PSI 协议的性能。在第一种情况下，和持有相同数量的输入元素。在第二种情况下，拥有比更大的集合，我们设定，。双方都不允许进行任何预计算。对于排序 - 比较 - 洗牌和基于 PWC 电路的协议，其复杂性取决于元素的比特长度，我们将（例如，对于 IPv4 地址的 PSI）。我们使用第 2.1 节中描述的长期安全参数。我们通过在一台机器上执行受信任的服务器和在第二台机器上执行希望计算交集的两个客户端，对 Kamara 等人（2014）的服务器辅助 PSI 协议进行基准测试。

实施方案：基于盲化 RSA（Cristofaro 和 Tsudik 2010）和混淆布隆过滤器（Dong 等人，2013）协议的实现取自作者，但我们使用哈希表来计算盲化 RSA 协议中找到交集的最后一步（原始实现使用了具有二次运行时间开销的配对比较），以及 Asharov 等人（2013）对布隆过滤器协议的 OT 扩展实现。我们在 C++ ABY 框架（Demmler 等人，2015）中使用了最先进的姚氏混淆电路和 GMW 协议实现，该框架实现了点对点（Malkhi 等人，2004）、半门（Zahur 等人，2015）、自由（Kolesnikov 和 Schneider，2008）、固定密钥混淆（Bellare 等人，2013）以及 OT 扩展（Asharov 等人，2013）。对于姚的混淆协议，我们评估了排序 - 比较 - 洗牌电路的大小优化版本（大小和深度为 σ 的比较电路），而对于 GMW，我们评估了深度优化版本（大小为，深度为的比较电路），用于位输入值（Schneider 和 Zohner 2013）。我们将 Kamara 等人（2014）的服务器辅助 PSI 协议的 PRP 和 CRF 实例化为固定密钥 AES-128 的（2 1）-OT 扩展，并将 RO 和 CRF 实例化为 SHA-256 的选的 OT 扩展。我们在选的 OT 中使用 SHA-256 而不是 AES 来实例化 CRF，因为它需要处理位长度的输入，而 AES 在使用固定密钥 AES-128 时只允许处理位的输入，在使用 AES-256 的密钥计划时只允许处理位的输入（Dessouky 等人，2017）。我们使用 GMP 库（v. 5.1.2）实现 FFC（有限域加密），使用 Miracl 库（v. 5.6.1）实现 ECC，使用 OpenSSL（v. 1.0.1e）实现对称加密基元，并使用 Asharov 等人（2013）的 OT 扩展实现。我们在 FFC 中的所有操作都是在阶数为的子组中进行的，其中位。

我们认为，我们提供了一个公平的比较，因为所有的协议都是用相同的编程语言（C/C++）实现的，在相同的硬件上运行，并使用相同的基础库进行加密操作。

对于每个协议，我们测量了从启动程序到客户端输出相交元素的时间。所有的运行时间都是 10 次执行的平均数。

6.2.2 实验比较

我们评估了 PSI 协议在局域网环境中的经验性能，并给出了协议的具体通信。虽然局域网环境不一定代表 PSI 的真实环境，但它允许我们在一个几乎理想的网络环境中对协议进行基准测试，从而关注协议的计算复杂性。我们在图 3 中给出了元素集的分类，并在表 9 中描述了详细的运行时间，在表 10 中描述了通信。我们现在比较不同类型的 PSI 协议的性能，然后比较同一类型的 PSI 协议。

类型之间的比较：从图 3 中，我们可以观察到，除了基于 OT 的 PSI 协议外，同一类型的 PSI 协议具有相似的运行时间和通信。不安全的朴素散列协议和服务器辅助的 PSI 协议在计算和通信方面比其他 PSI 协议至少要好一个数量级。基于公钥的 PSI 协议只需要很少的通信（特别是 DH-ECC 协议），但运行时间最高。基于电路的 PWC 协议比基于公钥的协议有更快的运行时间，但需要两个数量级的通信，并且不能很好地扩展到大型集合。最后，基于 OT 的 PSI 协议在性能上有所不同：Dong 等人（2013）的 GBF 协议具有与基于电路的 PWC 协议类似的运行时间和通信，而我们的基于 OT 的 PSI 协议具有比公钥和基于电路的协议更快的运行时间，与基于电路的协议相比，需要至少少一个数量级的通信。在所有的 PSI 协议中，我们新颖的基于 OT 的 PSI 协议是最快的，而且需要的通信量与基于公钥的 PSI 协议差不多。

基于有限安全的 PSI：朴素的散列协议在运行时间和通信方面优于服务器辅助协议 2 倍之多。然而，这些协议的安全保障比我们描述的其他协议要弱。

基于公钥的 PSI：对于基于公钥的 PSI 协议，我们观察到 Meadows（1986）的基于 DH 的协议在使用有限域密码学（FFC）时优于 Cristofaro 和 Tsudik（2010）的基于 RSA 协议。基于 DH 协议的椭圆曲线加密法（ECC）实例化变得更加高效，比 FFC 实例化的效率高 2 倍。基于 ECC 协议的优势在于其通信复杂度，在所有 PSI 协议中最低（参见表 10）。我们注意到，这些协议的一个主要优势是它们的简单性，这使得它们相对容易实现。

基于电路的 PSI：这里我们比较了 Huang 等人（2012）的 SCS 电路，我们的 PWC 电路（第 4.2 节）和 OPRF 电路（第 4.3 节），使用姚的混淆电路和 GMW 进行评估。结果可以总结如下。

GMW 协议比姚的混淆电路协议快 2 倍左右，这是由于平衡通信的原因。随着集合大小的增加，PWC 电路的扩展性优于 SCS 和 OPRF 电路，对于个元素的集合，其效率至少是三倍。由于其简单的功能，PWC 电路可以扩展到更大的集合尺寸，甚至可以使用 GMW 处理两组个元素的集合。

基于 OT 的 PSI：Pinkas 等人（2014）的随机混淆布隆过滤器协议在运行时间和通信方面比 Dong 等人（2013）的优化混淆布隆过滤器变体提高了约 1.5 倍。

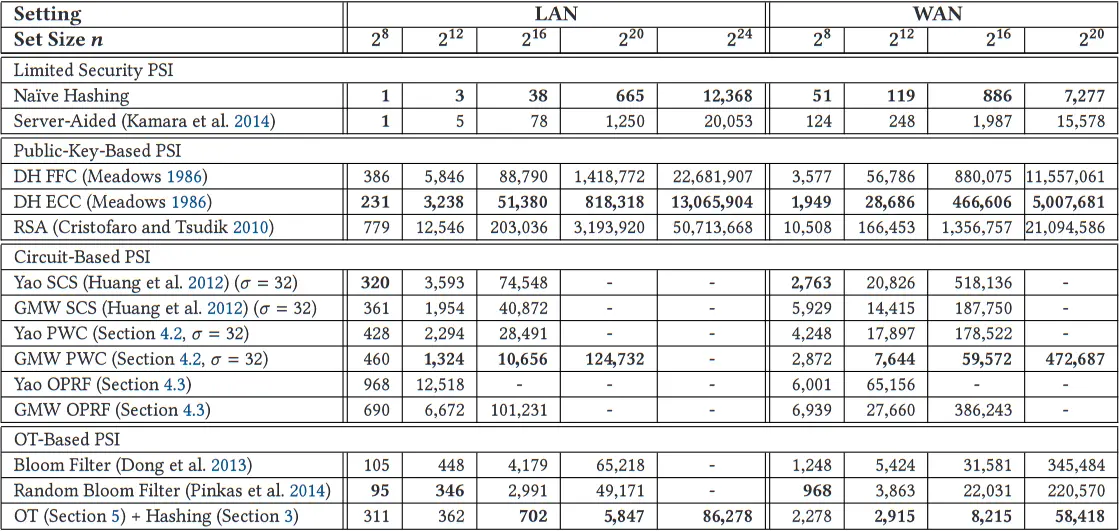
我们的基于 OT 的 PSI 协议在小集规模下的运行时间比基于布隆过滤器的协议都要高，因为选的 OT 扩展所需的基础 OT 的数量（以及公钥操作）是四倍以上。然而，这个工作量在安全参数中是线性的，并随着集合大小的增加而摊销。对于的更大的集合规模，我们基于 OT 的 PSI 协议在运行时间上比随机混淆布隆过滤器协议的效率高 9 倍，并且通信量减少 12 倍到 25 倍。

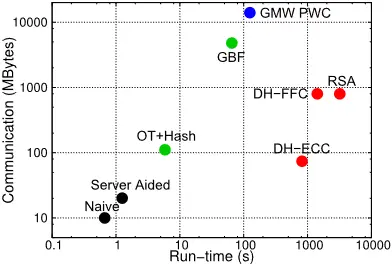
表 9. 在局域网和广域网设置中，一个线程的 PSI 协议的运行时间，单位为 ms。标示元素的位长。" " 表示执行过程中内存耗尽。每类中的最佳结果用粗体字标示。

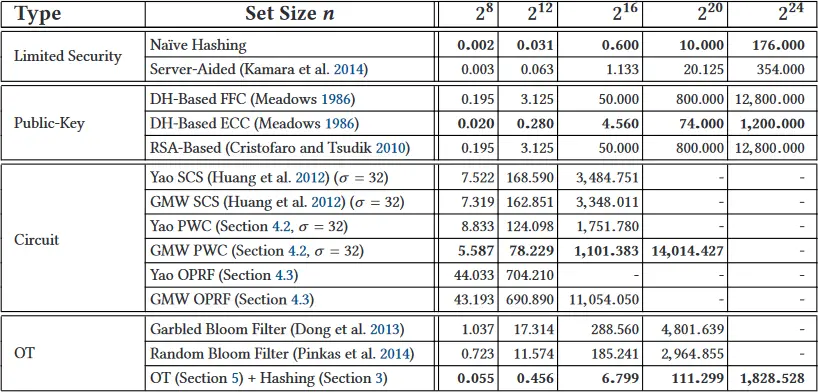
图 3. 个元素和位安全的 PSI 协议的运行时间（秒）和通信量（MB）。详细结果见表 9 和表 10。

表 10. 以 MB 为单位的 PSI 协议的通信量。标示元素的位长。" " 表示执行过程中内存耗尽。每类中的最佳结果用粗体字标示。

6.2.3 PSI 与不平等的设置尺寸

在许多 PSI 应用中，双方的集合大小是不相等的，通常一个拥有几百个元素集合的客户与一个拥有数百万条记录的数据库的服务器进行 PSI。我们在不平等的集合大小和的情况下，使用每一类中先前表现最好的协议进行 PSI：朴素散列、Kamara 等人的服务器辅助协议 (2014)，Meadows (1986) 的 DH-ECC 协议，第 4.2 节和第 4.3 节中的 PWC 和 OPRF 电路，以及第 5 节中我们的基于 OT 的 PSI 协议。我们评估了它们在局域网和广域网设置中的性能，并在表 12 中给出了结果的运行时间，在表 13 中给出了具体的通信。对于电路 PWC 协议和基于 OT 的 PSI 协议，它们都使用散列技术，我们使用表 11 中给出的参数。我们可以通过让将其哈希值发送给来大幅减少通信。然而，我们决定在一个一致的环境中对协议进行基准测试，在这个环境中，获得输出，而现有的两方 PSI 协议似乎都有一个与双方集合大小成线性的通信下限。

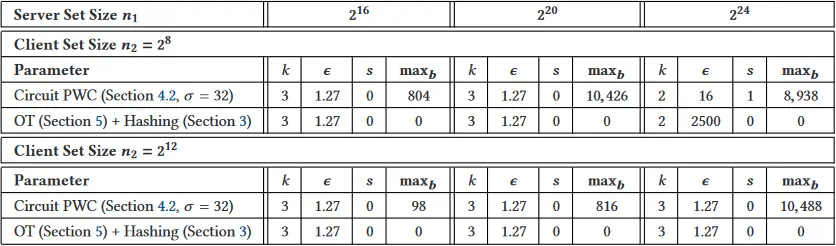
实验结果与相同集合大小的实验相似，但有一个明显的例外：OPRF 电路表现得非常好，实现了与服务器辅助协议相似的运行时间，甚至在和的情况下超过了朴素散列。OPRF 电路的这种良好性能可以用处理客户和服务器集合的不对称成本来解释。客户端集合中的每个元素都是通过使用通用安全计算技术安全评估 AES 电路来加密的，而服务器只需要使用固定密钥的 AES 对其集合中的每个元素进行加密，并将得到的密码文本发送给客户端。由于客户端的集合大小很小，通用安全计算技术的开销不会对整个运行时间产生很大影响。相比之下，朴素的散列协议使用 SHA-256 来处理元素，其速度比 AES 慢。

表 11. 在不等量集实验中使用的电路 PWC 和我们基于 OT 的 PSI 的参数

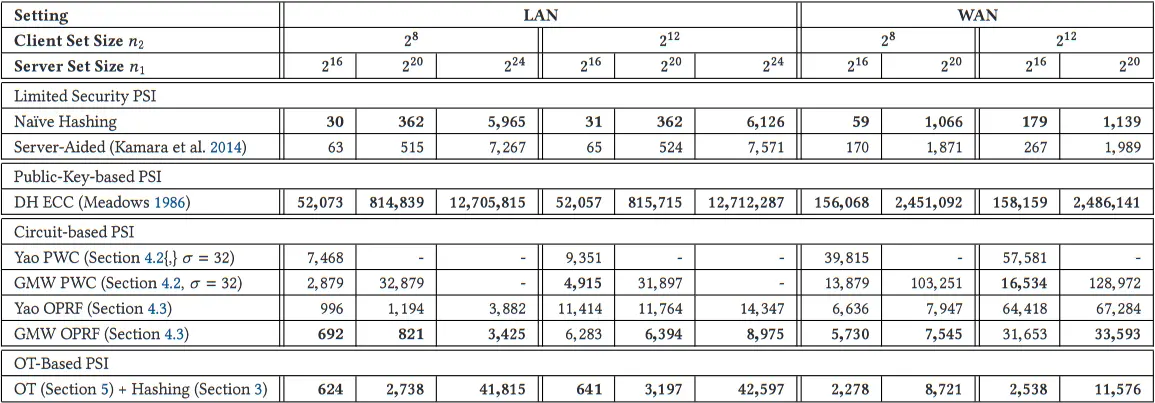
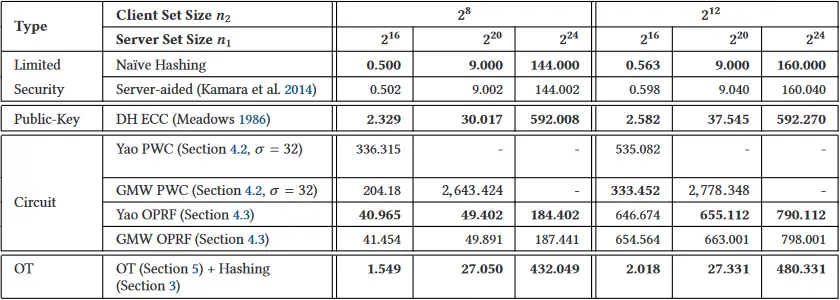
表 12. 在局域网和广域网设置中，PSI 协议的运行时间，以毫秒为单位，集合大小不等，。标示元素的位长。" " 表示执行过程中内存耗尽。每类中的最佳结果用粗体字标示。

表 13. 不等集尺寸的 PSI 的通信量（MB），。标示元素的位长。" " 表示执行过程中内存耗尽。每类中的最佳结果用粗体字标示。

6.2.4 十亿级别元素的 PSI

最后，我们通过对每个 10 亿位元素的集合进行评估来证明我们基于 OT 的 PSI 协议的可扩展性。对于这些规模，输入元素需要 16GB 的存储空间，这超出了我们服务器的主内存。相反，服务器将元素和中间值存储在他们的固态驱动器（SSD）上。我们还将朴素的散列协议作为性能的基准线。我们避免添加更多的主内存来处理这些集合，尽管这是最简单的解决方案，因为我们对协议的性能感兴趣，如果数据需要存储在 SSD 上。

为了计算 20 亿元素集的交集，朴素散列需要 74 分钟，其中 19 分钟（26%）用于散列和传输数据，55 分钟（74%）用于计算明文交集。我们基于 OT 的 PSI 协议总共需要 34.2 小时，其中 30.0 小时（88%）用于简单散列（布谷鸟散列并行运行，需要 16.3 小时），3 小时（9%）用于计算 OT，1.2 小时（4%）用于计算明文相交。

参考文献

A. Abadi, S. Terzis, and C. Dong. 2015. O-PSI: Delegated private set intersection on outsourced datasets. In ICT Systems Security and Privacy Protection (SEC’15) (IFIP AICT), Vol. 455. Springer, 3–17.

A. Abadi, S. Terzis, and C. Dong. 2017. VD-PSI: Verifiable delegated private set intersection on outsourced private datasets. In Financial Cryptography and Data Security (FC’16)(LNCS), Vol. 9603. Springer, 149–168.

M. R. Albrecht, C. Rechberger, T. Schneider, T. Tiessen, and M. Zohner. 2015. Ciphers for MPC and FHE. In Advances in Cryptology—EUROCRYPT’15 (LNCS), Vol. 9056. Springer, 430–454.

Y. Arbitman, M. Naor, and G. Segev. 2010. Backyard cuckoo hashing: Constant worst-case operations with a succinct representation. In Foundations of Computer Science (FOCS’10). IEEE, 787–796.

G. Asharov, Y. Lindell, T. Schneider, and M. Zohner. 2013. More efficient oblivious transfer and extensions for faster secure computation. In Computer and Communications Security (CCS’13). ACM, 535–548.

G. Asharov, Y. Lindell, T. Schneider, and M. Zohner. 2015. More efficient oblivious transfer extensions with security for malicious adversaries. In Advances in Cryptology—EUROCRYPT’15 (LNCS), Vol. 9056. Springer, 673–701.

N. Asokan, A. Dmitrienko, M. Nagy, E. Reshetova, A.-R. Sadeghi, T. Schneider, and S. Stelle. 2013. CrowdShare: Secure mobile resource sharing. In Applied Cryptography and Network Security (ACNS’13) (LNCS), Vol. 7954. Springer, 432–440.

P. Baldi, R. Baronio, E. De Cristofaro, P. Gasti, and G. Tsudik. 2011. Countering GATTACA: Efficient and secure testing of fully-sequenced human genomes. In Computer and Communications Security (CCS’11). ACM, 691–702. R.W. Baldwin andW. C. Gramlich. 1985. Cryptographic protocol for trustable matchmaking. In Symposium on Security and Privacy (S&P’85). IEEE, 92–100.

D. Beaver. 1996. Correlated pseudorandomness and the complexity of private computations. In Symposium on Theory of Computing (STOC’96). ACM, 479–488.

M. Bellare, V. Hoang, S. Keelveedhi, and P. Rogaway. 2013. Efficient garbling from a fixed-key blockcipher. In Symposium on Security and Privacy (S&P’13). IEEE, 478–492.

M. Bellare and P. Rogaway. 1993. Random oracles are practical: A paradigm for designing efficient protocols. In Computer and Communications Security (CCS’93). ACM, 62–73.

J. Boyar and R. Peralta. 2010. A new combinational logic minimization technique with applications to cryptology. In Symposium on Experimental Algorithms (SEA’10) (LNCS), Vol. 6049. Springer, 178–189.

E. Bursztein, M. Hamburg, J. Lagarenne, and D. Boneh. 2011. OpenConflict: Preventing real timemap hacks in online games. In Symposium on Security and Privacy (S&P’11). IEEE, 506–520.

H. Carter, C. Amrutkar, I. Dacosta, and P. Traynor. 2013. For your phone only: Custom protocols for efficient secure function evaluation on mobile devices. J. Secur. Commun. Netw. (2013).

E. De Cristofaro, J. Kim, and G. Tsudik. 2010. Linear-complexity private set intersection protocols secure in malicious model. In Advances in Cryptology—ASIACRYPT’10 (LNCS), Vol. 6477. Springer, 213–231.

E. De Cristofaro and G. Tsudik. 2010. Practical private set intersection protocols with linear complexity. In Financial Cryptography and Data Security (FC’10) (LNCS), Vol. 6052. Springer, 143–159.

S. K. Debnath and R. Dutta. 2015. Secure and efficient private set intersection cardinality using bloom filter. In Information Security Conference (ISC’15) (LNCS), Vol. 9290. Springer, 209–226.

D. Demmler, T. Schneider, and M. Zohner. 2015. ABY: A framework for efficient mixed-protocol secure two-party computation. In Network and Distributed System Security (NDSS’15). The Internet Society.

G. Dessouky, F. Koushanfar, A.-R. Sadeghi, T. Schneider, S. Zeitouni, and M. Zohner. 2017. Pushing the communication barrier in secure computation using lookup tables. In Network and Distributed System Security (NDSS’17). The Internet Society.

M. Dietzfelbinger, A. Goerdt,M.Mitzenmacher, A. Montanari, R. Pagh, and M. Rink. 2010. Tight thresholds for cuckoo hashing via XORSAT. In International Colloquium on Automata, Languages and Programming (ICALP’10) (LNCS), Vol. 6198. Springer, 213–225.

C. Dong, L. Chen, and Z. Wen. 2013. When private set intersection meets big data: An efficient and scalable protocol. In Computer and Communications Security (CCS’13). ACM, 789–800.

M. Fischlin, B. Pinkas, A.-R. Sadeghi, T. Schneider, and I. Visconti. 2011. Secure set intersection with untrusted hardware tokens. In Cryptographers’ Track at the RSA Conference (CT-RSA’11) (LNCS), Vol. 6558. Springer, 1–16.

M. J. Freedman, C. Hazay, K. Nissim, and B. Pinkas. 2016. Efficient set intersectionwith simulation-based security. J. Cryptol. 29, 1 (2016), 115–155.

M. J. Freedman, Y. Ishai, B. Pinkas, and O. Reingold. 2005. Keyword search and oblivious pseudorandom functions. In Theory of Cryptography Conference (TCC’05) (LNCS), Vol. 3378. Springer, 303–324.

M. J. Freedman, K. Nissim, and B. Pinkas. 2004. Efficient private matching and set intersection. In Advances in Cryptology— EUROCRYPT’04 (LNCS), Vol. 3027. Springer, 1–19.

O. Goldreich. 2004. Foundations of Cryptography. Vol. 2: Basic Applications. Cambridge University Press, Cambridge, UK.

O. Goldreich, S. Micali, and A. Wigderson. 1987. How to play any mental game or a completeness theorem for protocols with honest majority. In Symposium on Theory of Computing (STOC’87). ACM, 218–229.

G. Gonnet. 1981. Expected length of the longest probe sequence in hash code searching. J. ACM 28, 2 (1981), 289–304.

C. Hazay and Y. Lindell. 2008. Constructions of truly practical secure protocols using standard smartcards. In Computer and Communications Security (CCS’08). ACM, 491–500.

W. Henecka and T. Schneider. 2013. Faster secure two-party computation with less memory. In Symposium on Information, Computer and Communications Security (ASIACCS’13). ACM, 437–446.

Y. Huang, P. Chapman, and D. Evans. 2011. Privacy-preserving applications on smartphones. In Hot topics in Security (HotSec’11). USENIX.

Y. Huang, D. Evans, and J. Katz. 2012. Private set intersection: Are garbled circuits better than custom protocols? In Network and Distributed System Security (NDSS’12). The Internet Society.

Y. Huang, D. Evans, J. Katz, and L. Malka. 2011. Faster secure two-party computation using garbled circuits. In USENIX Security Symposium 2011. USENIX, 539–554.

B. A. Huberman,M. Franklin, and T.Hogg. 1999. Enhancing privacy and trust in electronic communities. In ACMConference on Electronic Commerce (EC’99). ACM, 78–86.

Y. Ishai, J. Kilian, K. Nissim, and E. Petrank. 2003. Extending oblivious transfers efficiently. In Advances in Cryptology— CRYPTO’03 (LNCS), Vol. 2729. Springer, 145–161.

S. Kamara, P. Mohassel, M. Raykova, and S. Sadeghian. 2014. Scaling private set intersection to s-element sets. In Financial Cryptography and Data Security (FC’14) (LNCS), Vol. 8437. Springer, 195–215.

A. Kirsch, M. Mitzenmacher, and U. Wieder. 2009. More robust hashing: Cuckoo hashing with a stash. SIAM J. Comput. 39, 4 (2009), 1543–1561. Á. Kiss, J. Liu, T. Schneider, N. Asokan, and B. Pinkas. 2017. Private set intersection for unequal set sizes with mobile applications. Privacy Enhancing Technologies (PoPETs’17) 2017, 4 (2017), 97–117.

L. Kissner and D. Song. 2005. Privacy-preserving set operations. In Advances in Cryptology—CRYPTO’05 (LNCS), Vol. 3621. Springer, 241–257.

V. Kolesnikov and R. Kumaresan. 2013. Improved OT extension for transferring short secrets. In Advances in Cryptology— CRYPTO’13 (2) (LNCS), Vol. 8043. Springer, 54–70.

V. Kolesnikov, R. Kumaresan, M. Rosulek, and N. Trieu. 2016. Efficient batched oblivious PRF with applications to private set intersection. In Computer and Communications Security (CCS’16). ACM, 818–829.

V. Kolesnikov and T. Schneider. 2008. Improved garbled circuit: Free XOR gates and applications. In International Colloquium on Automata, Languages and Programming (ICALP’08) (LNCS), Vol. 5126. Springer, 486–498.

M. Lambæk. 2016. Breaking and Fixing Private Set Intersection Protocols. Cryptology ePrint Archive, Report 2016/665. (2016). http://ia.cr/2016/665.

D. Malkhi, N. Nisan, B. Pinkas, and Y. Sella. 2004. Fairplay—A secure two-party computation system. In USENIX Security Symposium 2004. USENIX, 287–302.

C. Meadows. 1986. A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In Symposium on Security and Privacy (S&P’86). IEEE, 134–137.

G. Mezzour, A. Perrig, V. D. Gligor, and P. Papadimitratos. 2009. Privacy-preserving relationship path discovery in social networks. In Cryptology and Network Security (CANS’09) (LNCS), Vol. 5888. Springer, 189–208.

M. D. Mitzenmacher. 2001. The power of two choices in randomized load balancing. IEEE Trans. Parallel Distrib. Syst. 12, 10 (2001), 1094–1104. Robert H. Morelos-Zaragoza. 2006. The Art of Error Correcting Coding. Wiley, Hoboken (New Jersey), US. Code generation tools: http://eccpage.com.

R. Motwani and P. Raghavan. 1995. Randomized Algorithms. Cambridge University Press, New York, NY.

S. Nagaraja, P. Mittal, C.-Y.Hong, M. Caesar, and N. Borisov. 2010. BotGrep: Finding P2P bots with structured graph analysis. In USENIX Security Symposium 2010. USENIX, 95–110.

M. Nagy, E. De Cristofaro, A. Dmitrienko, N. Asokan, and A.-R. Sadeghi. 2013. Do I know you? – Efficient and privacypreserving common friend-finder protocols and applications. In Annual Computer Security Applications Conference (ACSAC’13). ACM, 159–168.

M. Naor and B. Pinkas. 2001. Efficient oblivious transfer protocols. In SIAM Symposium On Discrete Algorithms (SODA’01). Society for Industrial and Applied Mathematics (SIAM’01), 448–457.

A. Narayanan, N. Thiagarajan, M. Lakhani, M. Hamburg, and D. Boneh. 2011. Location privacy via private proximity testing. In Network and Distributed System Security (NDSS’11). The Internet Society.

J. B. Nielsen, P. S. Nordholt, C. Orlandi, and S. S. Burra. 2012. A new approach to practical active-secure two-party computation. In Advances in Cryptology – CRYPTO’12 (LNCS), Vol. 7417. Springer, 681–700. NIST. 2012. NIST Special Publication 800-57, Recommendation for Key Management Part 1: General (Rev. 3). Technical Report. National Institute of Standards and Technology (NIST), Gaithersburg (Maryland), US.

O. Oksuz, I. Leontiadis, S. Chen, A. Russell, Q. Tang, and B. Wang. 2017. SEVDSI: Secure, Efficient and Verifiable Data Set Intersection. Cryptology ePrint Archive, Report 2017/215. (2017). http://ia.cr/2017/215.

M. Orrù, E. Orsini, and P. Scholl. 2017. Actively secure 1-out-of-N OT extension with application to private set intersection. In Topics in Cryptology—CT-RSA’17 (LNCS), Vol. 10159. Springer, 381–396.

R. Pagh and F. F. Rodler. 2001. Cuckoo hashing. In European Symposium on Algorithms (ESA’01) (LNCS), Vol. 2161. Springer, 121–133.

R. Pagh and F. F. Rodler. 2004. Cuckoo hashing. J. Algorithms 51, 2 (2004), 122–144.

B. Pinkas, T. Schneider, G. Segev, and M. Zohner. 2015. Phasing: Private set intersection using permutation-based hashing. In USENIX Security Symposium 2015. USENIX, 515–530. http://eprint.iacr.org/2015/634.

B. Pinkas, T. Schneider, N. P. Smart, and S. C. Williams. 2009. Secure two-party computation is practical. In Advances in Cryptology—ASIACRYPT’09 (LNCS), Vol. 5912. Springer, 250–267.

B. Pinkas, T. Schneider, and M. Zohner. 2014. Faster private set intersection based on OT extension. In USENIX Security Symposium 2014. USENIX, 797–812. http://eprint.iacr.org/2014/447.

M. Raab and A. Steger. 1998. “Balls into bins”—A simple and tight analysis. In Randomization and Approximation Techniques in Computer Science (RANDOM’98) (LNCS), Vol. 1518. Springer, 159–170.

P. Rindal and M. Rosulek. 2016. Faster malicious 2-party secure computation with online/offline dual execution. In USENIX Security Symposium 2016. USENIX.

P. Rindal and M. Rosulek. 2017a. Improved private set intersection against malicious adversaries. In Advances in Cryptology—EUROCRYPT’17 (LNCS), Vol. 10210. Springer, 235–259.

P. Rindal and M. Rosulek. 2017b. Malicious-secure private set intersection via dual execution. Forthcoming. In Computer and Communications Security (CCS’17). ACM.

T. Schneider and M. Zohner. 2013. GMW vs. Yao? Efficient secure two-party computation with low depth circuits. In Financial Cryptography and Data Security (FC’13) (LNCS), Vol. 7859. Springer, 275–292.

R. Schürer and W. Schmid. 2006. Monte Carlo and Quasi-Monte Carlo Methods 2004. Springer, Chap. MinT: A Database for Optimal Net Parameters, 457–469.

A. Shamir. 1980. On the power of commutativity in cryptography. In International Colloquium on Automata, Languages and Programming (ICALP’80) (LNCS), Vol. 85. Springer, 582–595.

S. Tamrakar, J. Liu, A. Paverd, J.-E. Ekberg, B. Pinkas, and N. Asokan. 2017. The circle game: Scalable private membership test using trusted hardware. In Computer and Communications Security (ASIACCS’17). ACM, 31–44.

A. C. Yao. 1986. How to generate and exchange secrets. In Foundations of Computer Science (FOCS’86). IEEE, 162–167.

S. Zahur, M. Rosulek, and D. Evans. 2015. Two halves make a whole: Reducing data transfer in garbled circuits using half gates. In Advances in Cryptology—EUROCRYPT’15 (LNCS), Vol. 9057. Springer, 220–250.