On Deploying Secure Computing - Private Intersection-Sum-with-Cardinality

发表于 更新于 分类于

论安全计算的部署：具有 Cardinality 的隐私集合交集求和问题

在这项工作中，我们讨论了我们在行业内部署加密安全计算协议的成功努力。我们考虑的问题是隐私计算广告活动的总转换率。这个基础功能可以被抽象为具有 Cardinality 的隐私交集和（PI-Sum）。在这种情况下，两方持有包含用户标识符的数据集，其中一方还拥有与其每个用户标识符相关的整数值。双方希望了解他们共同拥有的标识符的数量以及与这些用户相关的整数值的总和，而不透露任何有关他们私人输入的信息。

我们确定了主要的特性和有利因素，这些特性和因素使得部署一个加密协议成为可能、实用，并被独特地定位为手头任务的一个解决方案。我们描述了我们的部署环境和最相关的效率衡量标准，在我们的环境中，它是通信开销而不是计算。我们还提出了一个货币成本模型，可以作为一个统一的成本衡量标准，以及反映我们使用情况的计算模型：一个低优先级的批量计算。

我们提出了三个带 cardinality 的 PI-Sum 协议：我们目前部署的协议，它依赖于 Diffie-Hellman 风格的双重掩码，以及两个新的协议，它们利用了最近的私有集相交（PSI）技术，使用不经意传输和加密的布隆过滤器。当用不同的加法同态加密方案进行实例化时，我们将后面两个协议与我们的原始解决方案进行比较。我们实现了我们的构造并比较了它们的成本。我们还与最近用于计算两个数据集的交集的通用方法进行了比较，结果表明，我们最好的协议的货币成本比已知的最佳通用方法低 20 倍。

1 介绍

安全的多方计算 (MPC) 长期以来一直致力于实现对来自多个来源的数据的联合分析，同时保持每个输入源的隐私。在过去的十年中，该领域的最新发展显示了令人印象深刻的效率改进，表明这一承诺超越了可行性的结果，进入了实际的实施。然而，这种技术在实际工业环境中的应用却非常有限。 在本文中，我们介绍了我们在一个特定的商业应用中使用加密 MPC 技术的工作：归属总的广告转换。我们的解决方案已经在实践中使用了几年，在本文中我们讨论了我们在这个问题上部署和使用 MPC 解决方案所遇到的各种限制，以及这些限制如何影响我们选择实施的加密协议。我们的应用问题与私有集交集（PSI）问题有相似之处，但我们需要的确切功能是 PSI 问题的扩展，我们称之为有心性的私有集交集和。然而，由于 PSI 的技术水平已经有了巨大的进步 [11]、[31]、[37]、[47]、[49]、[51]、[55]，通常以我们的商业场景作为实际应用的例子，在这项工作中，我们考虑最近有效的 PSI 构建方法以及如何将它们扩展到我们设置的解决方案。在低优先级的 "批量计算" 环境中执行时，我们将这些构造的效率成本与我们原来的解决方案的效率成本进行比较，因为在这种环境中不需要实时得到结果。我们通过使用云供应商对计算和网络资源收取的价格来模拟货币成本，我们发现这是对我们部署环境中的成本的良好近似。这种约束与安全计算领域的大多数工作所考虑的约束不同，这些工作通常侧重于最小化端到端的运行时间。

广告转换：当用户在某个网站上看到某个公司的在线广告，然后在该公司的商店里进行购买时，就会发生广告转换。投放广告的公司想知道它有多少收入可以归功于其在线广告活动。然而，计算这些归因统计所需的数据是由两方分担的：广告供应商和公司，前者知道哪些用户看过某个特定的广告，后者知道谁购买了产品以及他们花了多少钱。这两方可能不愿意或无法公开基础数据，但双方仍希望计算出一个总体的人口水平测量：有多少用户看到了广告并进行了相应的购买，以及这些用户总共花费了多少钱。他们希望在做到这一点的同时，确保在输入的数据集中，除了这些总量值之外，没有任何关于个人用户的信息被披露。

具有 Cardinality 的隐私集合交集求和：抽象地讲，上述问题可以被看作是私有集交集问题的一个变种，我们称之为具有 Cardinality 的隐私集合交集求和问题。在这种情况下，有两方拥有由标识符组成的私有输入集，其中一方还拥有与每个标识符相关的整数值。双方希望了解两个输入集的交集中所有标识符的相关整数值的总和，以及交集的 cardinality（或大小），但除此之外就没有了。特别是，任何一方都不应该了解交集中的实际标识符，也不应该了解关于另一方数据的任何额外信息（除了他们的输入集的大小），例如比交集上的总数更细的相关值。此外，双方可以选择以交集的最小阈值大小为条件来揭示交集的总和。

对于广告转换测量用例，一方持有的标识符对应于看过广告活动的用户，而另一方持有的标识符和整数值分别对应于购买相关物品的用户和他们花费的金额。虽然广告转换问题是一个可以用隐私集合交集求和协议解决的例子场景，但这个功能的适用范围更广。它可以很容易地扩展到其他统计数据，如平均值和方差。更广泛地说，PSI-Sum 协议提供了一个安全的解决方案，适用于任何一方持有关于用户的私人统计数据，另一方持有关于特定人群中的用户成员的私人知识，并且双方都想了解该特定人群的总体统计数据的情况。例如，人们可以回答这样的问题："服用特定药物的病人的平均血压是多少？" 或 "居住在特定邮政编码的人的住房拥有率是多少？"。

贡献：我们的贡献有两个方面。首先，我们详细描述了我们的部署，包括我们选择解决方案的约束和限制因素。这包括讨论安全聚合广告转换业务问题的特点，使其成为基于加密的 MPC 解决方案的良好候选。这些因素包括隐私需求和强大的商业利益，但也包括使用有效技术的问题的可操作性。该解决方案的关键制约因素是简单性和可解释性，以及易于实施、易于维护和可扩展性。

我们讨论了我们部署的协议的细节，该协议基于 [41] 的经典集合交叉协议，该协议使用 Pohlig-Hellman 密码（基于 Decisional Diffie-Hellman（DDH）的难度）-- 该功能也可以被视为具有共享密钥的不经意 PRF [34]。聚合属性是通过使用加法同态加密实现的。我们描述了典型的日常工作负载，以及运行这些工作负载的成本，包括货币成本。我们观察到，我们的应用不是实时的，可以使用廉价的低优先级的、可抢占的计算。在这种 "批量计算" 的环境中，带宽仍然是一种稀缺的共享资源，多个应用程序都在竞争（各种云供应商的资源价格见表 1）。因此，通信复杂度成为我们协议最相关的效率衡量标准。我们相信，我们的见解对那些试图将安全计算技术用于实践的人来说是有用的。

作为我们的第二个主要贡献，我们通过最近大量改善高效 PSI 协议现状的论文 [11], [31], [37], [47], [49], [51], [55] 的视角，重新审视了具有 Cardinality 的隐私集合交集求和问题，以便将潜在的新解决方案的效率成本与我们部署的实现中使用的 DDH 风格协议进行比较。 我们的目标是看更多的现代技术是否能以增加复杂性为代价导致显著的节省。为此，我们将成本与最近的一套基于混淆电路式的技术 [11]、[31]、[32]、[51] 进行比较，这些技术明确考虑了交点上的隐私计算功能，并且可以直接扩展到计算我们的功能。我们还研究了最近计算隐私集合交集的方法 [17], [20], [22], [37], [47], [49], 并试图使它们适应于计算具有 Cardinality 的隐私集合交集求和。

虽然最初的具有 Cardinality 的隐私集合交集求和功能看起来非常接近 PSI 功能，它安全地计算两个输入集的交集，但事实证明，在隐藏交集的同时实现额外的聚合是有效率成本的。同时，PSI 功能是扩展功能的安全协议中的一个隐含的必要构件。因此，最近的 PSI 方法 [17]、[20]、[22]、[37]、[47]、[49] 需要明显不同的技术，以适应有 cardinality 的 PSI-Sum 设置。我们将调整工作集中在这些工作中的两个主要方法上。第一种是基于随机不经意传输，并建立在 [49] 和 [37] 所开发的技术上。这种方法利用了不经意 PRF 技术（OPRF），我们在两步不经意评估中对其进行了扩展，允许对评估的输入进行秘密置换。这使我们能够隐藏交集中的元素的身份。为了促进聚合功能，我们利用了加法同态加密，正如我们部署的协议一样。第二个协议是基于加密布隆过滤器的，并受到最近几个 PSI 解决方案的启发 [17]、[20]、[22]。我们构建了一个不经意协议，用于在加性同态加密下评估加密布隆过滤器的成员资格。我们还使用加性同态加密来实现聚合功能。除了这两个新的构造，我们还给出了一个配方，用于将一个普通形式的 PSI 协议转换为计算具有 Cardinality 的隐私集合交集求和的协议。我们称这个配方为 "标签、洗牌、聚合"，并认为它适用于一类广泛的较新的方法。

此外，在我们上面总结的两个新的隐私集合交集求和协议，以及我们部署的协议中，输出接收方是拥有输入标识符和值对的一方。我们还构建了协议的 "反向" 变体，将输出接收方改为只有标识符的输入集的一方。我们所有的构造都实现了安全的计算功能，并对半诚实的对手具有安全性。

所有三个协议都使用加法同态加密（HE）作为构建模块。虽然我们部署的实现使用了 Paillier [46] 加密，并由于 Damgard-Jurik [16] 的优化，这在当时提供了最好的效率保证，但最近基于格子的构造的效率有了很大的提高 [8]、[9]、[24]、[29]。我们将这两种方案与现有的第三种加法同态加密方案 ElGamal [23] 一起考虑，以进行综合比较，并分析我们的协议在与每个加法 HE 方案实例化时的效率权衡。

我们实现了我们所描述的每一个协议，并对它们在计算、通信和货币成本方面的性能进行了比较，同时也与最近使用混淆电路式技术对两个数据集的交集进行通用计算的协议进行了比较 [11]、[31]、[50]。我们发现，在这些协议中，使用 Paillier 作为同态加密的 DDH 式协议实现了最低的货币成本，在 10 万个元素的输入集上需要 0.084 美分（USD）。我们还发现，我们针对 PI-Sum 的 DDHstyle 协议的变体，使用 RLWE 同态加密的关联值，在大小为 100,000 的集合上花费的时间少了约 40%（47.4 秒对 74.4 秒），货币成本减少了 11%，为 0.075 美分。此外，我们所有的协议（DDH、ROT 和布隆 Filter）在货币成本方面都超过了 [11] 和 [31] 的通用方法。[50] 的方法优于我们基于布隆过滤器的解决方案，但在货币成本上比基于 ROT 和 DDH 的解决方案更昂贵。总的来说，在我们已经确定的限制条件下，部署的 DDH 协议仍然是我们的最佳选择。具体来说，基于部署的 DDH 协议的货币成本比任何基于混淆电路的新型通用方法都要便宜 20 倍。

路线图：在第 2 节中，我们详细讨论了我们问题的实际设置。在第 3 节中，我们给出了我们所部署的协议的细节。在第 4 节中，我们根据 PSI 的最新进展，重新审视了具有 Cardinality 的隐私集合交集求和问题。我们概述了最近的 PSI 方法，并在第 4.2 节中提出了将 PSI 协议转化为具有 Cardinality 的隐私集合交集求和的秘诀。在第 4.3 节中，我们提出了两个使用新技术的新构造。我们所有的构造都使用了附录 A 中定义的几个加密基元。在第 5 节中，我们介绍了我们的协议实现的测量结果，包括基于货币成本与基于混淆电路技术的工作进行比较。在附录 A 中，我们给出了各种有用的符号和定义。在附录 B 中，我们讨论了使用不同加密方案来实例化我们的协议的权衡。

2 问题的设定

我们现在描述问题的细节和我们的部署环境，包括正式的问题陈述和它的特点，我们的执行环境和日常工作负载的估计，以及我们用于协议的货币成本模型。

2.1 正式的问题陈述

在图 1 中，我们给出了一个关于我们旨在安全计算的功能的正式描述。在附录 G 中，我们还描述了一个反向的变体，即 代替 学习交集和 。

我们的部署还假设各方已经拥有具有相同标识符空间的数据。寻找一个适当的共同标识符空间是一个重要的问题，与当前的工作正交。

保护个体价值。 功能显示了交集中的记录的集合值。如果没有离群值，那么这个集合就为被添加的单个值提供了高水平的隐私保护。保护可能被总和揭示的离群值的一种方法是将离群值从输入数据集中删除。类似的问题发生在低阶数字上，对此我们可以使用四舍五入。对于许多应用场景，这些保护措施可以提供足够的隐私保证。对于这些不足够的设置，各方可以在计算的输出中添加差分隐私噪音 [21]。

图 1

图 1： ：具有 Cardinality 功能的私有交集 - 和。

2.2 问题特征和制约因素

在这一节中，我们讨论了我们的部署所解决的业务问题的各种特征，即计算广告转化率指标。我们首先考虑使该问题适合于安全计算解决方案的特点。

强大的商业利益：鉴于加密解决方案增加了大量的复杂性和效率成本，明确的商业利益是探索此类解决方案的前提条件。广告活动转化率的测量对广告商来说至关重要，使他们能够更有效地部署其营销预算。

强烈的隐私需求：对于我们的应用，计算分析所需的数据被分割给不同的当事方，每个当事方都有强烈的愿望来保持他们的数据的私密性。这是寻找具有强大隐私属性的解决方案的一个强大动力。

替代品带来了不理想的风险：各方可能有与底层数据相关的限制，使得替代方案，如使用受信任的第三方或开发隔离的执行环境，不那么令人满意或不可接受。当没有其他解决方案可以接受时，相对昂贵的加密解决方案会变得更有吸引力，因为它提供了所需的端到端隐私。

可行性：底层问题必须适合于有效的解决方案。现有的高效私人集合相交解决方案是一个很好的迹象，表明我们的应用所依据的私人相交和问题将是可操作的。

非实时性：一个应用程序的输出不是实时需要的（如分析、学习等），可以更容易容忍与加密解决方案相关的开销成本。

设计约束条件：接下来我们将讨论我们问题的各种设计约束。我们注意到，我们的背景是跨多个企业的安全计算（通过广域网 - WAN）。单个企业内部的安全计算，或者同一公司的服务器和移动应用程序之间的安全计算的特点可能是不同的。在此前提下，我们根据以下特点做出了解决方案的决定。

通信效率：也许令人惊讶的是，对于我们考虑的离线 "批量计算" 场景，通信成本远比计算更重要。对于涉及多个企业的安全协议来说，尤其如此，在这种情况下，服务器不能同地办公（广域网解决方案）。网络成本比计算成本高一个数量级，这反映在云供应商收取的费用中（见表 1）。

被充分理解的工具和假设：当涉及到部署新的密码学时，公司往往是高度规避风险的，因此，拥有使用被充分理解的基本假设和广泛分布的实施的协议是非常有帮助的。

简单性：在实际部署中，特别是涉及多个企业的部署中，简单性的重要性怎么强调都不过分。一个简单的协议更容易向所涉及的多个利益相关者解释，并大大简化了使用一项新技术的决定。它也更容易在没有错误的情况下实施，测试，审计正确性，以及修改。它通常也更容易通过并行化或以分布式的方式进行优化。简单性还有助于长期的维护，因为随着时间的推移，越来越多的人需要了解一个解决方案的工作细节。相反，一个解决方案越复杂，在上面提到的各种情况下就会出现更多障碍。

灵活性：任何成功的部署都可能推动对相关问题解决方案的需求。依靠 API 的模块化设计，可以在解决整类问题的过程中重复使用，这始终是可取的。

2.3 对抗模型

另一个重要的设计轴是安全计算应该保护哪一类恶意行为。

我们可以用各种不同的模型来设计我们的协议，其中两个极端是完全信任和恶意对手模型。完全信任意味着各方相信对方会在明确的情况下正确计算数据，并在协议结束后删除数据。另一方面，恶意对手被允许任意地偏离任何规定的协议。在这两个极端之间存在中间概念，其中一个重要的概念是针对诚实但好奇的对手的安全性。提供 "诚实可信"（或半诚实）安全的协议，（在 [58] 中建模）假定参与者将诚实地遵循协议步骤，但可能试图从各种协议消息的记录本和日志中尽可能多地了解。

虽然对更强大的对手的保护自然更有吸引力，但它确实伴随着大量的效率成本（尤其是通信）。此外，加密协议的安全模型是全面风险分析的一部分，其中包括各方偏离的动机、基础数据的性质、互动各方之间的信任规模和水平，以及外部执行机制的可用性，如合同或代码审计。与恶意安全模型的协议相比，半诚实模型有相对有效的解决方案可用，特别是在通信成本和货币成本方面。它也是对完全信任模型的重大改进，该模型依靠外部非加密机制来确保隐私。特别是，半诚实模型对任何一方的数据泄露都给予了强有力的隐私保护，因为，由于半诚实的协议日志在规定的协议输出之外没有任何泄露。

在我们的部署中，考虑到所有因素，我们选择了 "半诚实" 的安全目标。

2.4 工作负载和执行环境

我们部署的一个典型的日常工作负载涉及每对当事人之间约 个协议的执行，每个执行涉及每方输入中的 个项目。

我们的应用不是实时的，因此我们的部署环境是对延迟不敏感的批量计算的代表。每一方都控制着自己的计算和存储资源，此外，双方都可以访问共享的存储资源，用于传输协议执行的中间步骤的数据。 个协议执行中的每一个都在共享存储中被分配了一个单独的目录。每当一方完成了某一特定执行的回合，它就将回合结果写入该执行的共享目录中。每一方都以相对较长的延迟（几分钟左右）不断轮询共享存储中的这些目录，以检查是否有新的文件被写入，如果有，就执行相应协议的下一轮执行。执行以这种方式继续，直到所有的执行都完成。

各方在他们自己的数据中心执行他们的协议部分。中间协议数据在这些数据中心之间使用互联网上的标准 SSL 连接进行传输。

2.5 货币成本模型

我们使用协议执行的总货币成本作为我们的主要成本指标。

为什么是货币成本：我们的业务用例对延迟不敏感：输出的统计数据只需要用于生成定期报告。因此，传统上使用的执行的端到端运行时间并不是衡量成本的最重要标准（只要所有的执行能在一天内完成）。相反，资源的成本（CPU、内存，尤其是网络）才是最重要的。货币成本提供了一个方便的措施，以实际相关的方式统一这些不同资源的成本。

使用的具体费用：对于资源的具体货币成本，我们使用了谷歌平台对可抢占的虚拟机（包括 CPU 和内存）收取的成本，以及 "互联网出口" 网络使用的最便宜成本（代表流向外部数据中心或云供应商的数据）。

如表 1 所示，这些费用与其他云供应商收取的大宗费用范围相似。所示的价格是 AWS 和 Azure 的 2GB 内存的单 CPU 机器，以及谷歌云的 3.75GB 内存。网络带宽成本是针对 10-50TB 数据传输层的互联网出口。

与端到端运行时间相比，货币成本作为衡量标准的一个关键特征是，它对通信成本给予了很大的权重。一千兆字节的通信只会给端到端运行时间增加几分钟，但其货币成本相当于 8 小时的计算。

理由：即使我们的执行环境涉及各方在自己的数据中心运行协议，云计算的定价模型也密切反映了我们环境的相对资源成本。事实上，在我们的部署方案中，通信甚至受到更片面的限制。这反映了一个事实，即网络带宽是一种高度受限的资源，在一个数据中心增加更多的处理器比增加离开数据中心的总带宽要便宜得多。

替代成本模型：根据我们的经验，我们使用的成本模型密切代表了数据中心到数据中心的执行协议的成本，也代表了托管在不同云供应商的各方之间的成本。虽然我们不知道除了我们自己的安全计算部署之外，还有哪些企业对企业的安全计算部署，但我们预计数据中心对数据中心和云对不同的云是最常见的部署场景，因此使用云成本也会很适合那里。

如果两个参与者使用相同的云供应商，并在同一云区域内同地办公，网络成本会变得更便宜，而我们的部署并非如此。例如，在 GCP 内，同一地区的网络传输成本为每 GB 0.01，比互联网的出口率便宜 8 倍。在这种情况下，具有不同效率权衡的协议可能有更好的货币成本。

表 1

表 1: 计算和网络成本，由不同的云供应商收取。计算成本是指单个预先订购的可抢占的 CPU 和 2-4GB 的内存。网络成本是每个供应商的 10-50TB 的云到互联网出口流量的成本。该表是预先计划的、低优先级的资源成本的代表。

2.6 相关工作

在实践中部署安全计算是具有挑战性的，但也有一些现实世界的应用利用了 MPC。其中包括丹麦的甜菜拍卖 [6]、爱沙尼亚的一个金融应用 [5]、马萨诸塞州大学教师工资的安全调查 [39]，以及一个报告骚扰行为的平台 [54]。最近，Lindell 等人 [2]，[28] 为在单一组织拥有的机器之间运行的加密操作部署了安全计算。谷歌也报告了使用安全计算协议来聚合来自移动设备的本地训练的机器学习模型 [7]。然而，组织在多个实体或企业之间常规使用安全计算的情况仍然很少。

3 已部署的协议

在本节中，我们描述了我们部署的协议，即基于 DDH 的协议。

3.1 协议细节

在这里，我们提出了我们的基于 DDH 的相交和协议，这是我们针对上述限制条件而设计的。根据我们的理解，我们的协议是解决相交和问题的最简单的协议。它使用了众所周知的基于经典假设的加密基元，并可以从广泛部署的库（如 OpenSSL）中构建。它的目标是半诚实的安全，并旨在最大限度地减少通信成本。此外，它足够灵活，允许几个重要的变体。

我们的协议扩展了一个现有的 PSI 协议 [41]。它使用附录 A 中定义的下列基元：一个 DDH 假设成立的群组 ，一个加法同态加密方案（ , , ）和一个哈希函数 ，作为安全证明的随机预言机。我们在图 2 中展示了我们的结构。

在高层次上，双方互动，使用一个乘法共享的秘密指数，对其数据集中的每个条目进行散列和指数化。在这个互动过程中，被散列和指数化的值也被洗牌。因此，在最后，输出接收器是比较输入集的伪随机表示，以计算交集，而无法将其与原始输入值联系起来。我们的结构可以被看作是计算不经意的 ROM PRF [34]，其中密钥是乘法共享的，或者评估具有共享密钥的确定性的 Pohlig-Hellman 密码 [30]。我们应用 Pohlig-Hellman 密码的群组 可以是任何 DDH 假设成立的群组，并且允许散列到一个随机发生器。在图 2 中，为了简单起见，我们假设 有质数阶。

我们的协议扩展了 Meadows [41] 关于私密匹配和 Huberman [33] 关于交集心率的工作思路，以支持交集之和。为了实现这一点，持有相关价值的一方将 下的价值进行加法同态加密，而另一方则同态计算洗牌后的交集的价值之和。这个总和被送回给第一方，然后第一方解密以恢复交集的总和。

该协议的正确性立即从检查中得出，即 学会了交集和和 cardinality。

我们在下面陈述安全性的定理。诚实但好奇的模型中的正式安全证明出现在附录 D 中。他们表明，每一方只学到了交集大小和交集和。证明使用了一个标准的混合论证，表明每一方的观点可以通过用假值替换 "真实" 的协议值来模拟，同时保持相同的交集大小和，并且根据 DDH 的假定硬度和同态加密方案的安全性，假值与真实值是不可区分的。

定理 1（ 中针对 的 HBC 安全）：存在一个 模拟器 ，使得对于所有安全参数 和输入 ， ： 其中 是 的输入大小， 是相交集合， 是其 cardinality。

定理 2（ 中针对 的 HBC 安全）：存在一个 模拟器 ，使得对于所有安全参数 和输入 ， ： 其中 是 的输入大小， 是相交集合， 是相交集合的和。

图 2

图 2： ：我们部署的基于 DDH 的隐私集合交集求和协议。

基于 DDH 的隐私交集求和协议

  • 输入：

    • 两方：一个素数群 和一个标识符空间 。一个哈希函数 ，被建模为一个随机预言机，它将标识符映射到 的随机元素。
    • (Server)：集合 ，其中 。
    • (Client)：元组集合 ，其中 ， 。

  • 设置阶段：

    • 每方在群 中随机选择一个隐私指数 。
    • 为加法同态加密方案生成一个新的密钥对 ，并将公钥 发送给 。

  • 第一轮（ Server）：

    1. 对于其集合中的每个元素 ， 应用散列函数，然后用其密钥 进行指数化，从而计算出 。
    2. 按洗牌顺序将 发送给 。

  • 第二轮（ Client）：

    1. 对于上一步从 收到的每个元素 ， 使用其密钥 对其进行指数化，计算出 。
    2. 按洗牌顺序向 发送 。
    3. 对于其输入集中的每个项目 ， 将哈希函数应用于该对的第一个元素，并使用密钥 对其进行指数化。它使用加法同态加密密钥 对该对的第二个元素进行加密。这样它就计算出了这一对 和 。
    4. 将集合 按洗牌顺序发送给 。

  • 第三轮（ Server）：

    1. 对于第 2 轮第 4 步中从 收到的每一项 ， 用 对其第一个成员进行指数化，从而计算出 。

    2. 计算相交集 。

    其中 是第一轮中从 那里收到的集合。

    1. 对于交集中的所有项目， 同态地添加相关的密文，并计算出一个加密交集和的密文。

      然后， 使用 随机化密文，并将其发送给 。

  • 输出轮（ Client）： 使用秘钥 对第三轮收到的密文进行解密，以恢复交集之和 。

3.2 参数选择

在我们的部署中，我们使用 的实现 ，一个具有 位群元素的 椭圆曲线，作为群 。对于随机预言机，我们使用 应用于输入，并重新应用，直到产生的输出位于椭圆曲线上。为了在每次执行时模拟一个新的随机预言机，双方选择一个共同的随机种子，并在散列前将其预加到每个输入中。

对于加法同态加密方案，我们使用 位素数的 加密，采用 优化 [16]， 。因此，每个密文为 位，明文空间为 位。我们假设每个相关值最多为 位，包括求和之后，因此我们可以将许多值打包到一个密文中。开槽的细节可以在附录 B.1 中看到。在槽之间允许 位的屏蔽，并留出一半的明文空间以允许槽被移位和添加，我们可以将 个整数值打包到一个密文中。我们的 实现是建立在 的 库之上的。

3.3 部署成本

在表 2 中，我们给出了单次会话的通信和计算成本，其中每一方的数据库中有 个条目，以及 次这样的会议，这大致相当于一天的工作量。此外，我们使用表 1 中给出的 的资源估值给出了美元成本。运行时间是双方的总和，是在一台配备英特尔至强 CPU E5-1650 v3（3.50 GHz）的台式工作站的单核上测量的，这在我们的部署中是典型的机器，也是谷歌云平台的虚拟 CPU 的代表。

我们看到，尽管原始计算时间似乎相当大，而通信相对适中，但通信的成本要比美元成本高 倍，占协议货币成本的 75%。

表 2

表 2：具体的部署成本，对于每一方超过 100,000 条的单一协议执行，以及一天有 1,000 次这样的执行。货币成本的单位是美分（USD），使用表 1 中的 GCP 值来评估通信和计算。

3.4 变体

我们考虑了该协议在不同背景下的变体。这些变体对功能进行了修改，提供了重要的灵活性。

门限变体：一个变体是一个简单的门限变体，它允许 在第三轮中，如果相交大小太小，在计算相交之和之前，中止协议。

反向变体：图 2 中的协议让 在第 3 轮执行相交和同态相交和。该协议可以反过来，让 来执行交集和交集和，而 收到输出。为了实现这一点， 在第 3 轮中对每个加密的关联值进行加法掩码，并将其与洗牌后的集合 一起发送给 。然后， 解密并将与被屏蔽的洗牌交集相对应的值加在一起。然后， 可以利用它对掩码的了解来解除掩码的交集。请注意，这个变体与打包的加法同态加密不兼容。

分段输入：在某些情况下，最好将 的输入分成几个互不相干的部分，并让 学习每个部分的相交和。例如，在广告转换测量的用例中，段可能对应于不同的年龄组，或不同的地理区域。实现这一目标的方法之一是为 持有的每个细分市场运行一个单独的协议执行。然而，这大大增加了成本。一个简单的替代方法是， 在第一轮中按段分开发送其数值，而 只在一个段内洗牌，但不在不同段之间洗牌。这使得 能够计算出每个段的交集大小和加密的总和，其成本与单一的非分段执行大致相同。

多个相关值：该协议很容易推广到这样的情况： 数据中的每个项目都有多个相关的整数值，并且各方希望了解所有这些值的总和。这可以通过简单地将所有这些值打包到同态加密的不同槽中，并为每种类型的值创建一个和来处理。

通过额外发送原始相关值的平方，多个值也可以计算出交集之和的方差。双方将了解到交集大小、交集和和的平方，从中可以计算出方差。

4 重新审视这个问题：新协议

在这一节中，我们转向这项工作的第二个主要贡献，即根据 PSI 协议的大量最新进展，重新审视安全地计算具有 Cardinality 的隐私集合交集求和的问题。我们给出了两个基于新方法的新协议。此外，我们描述了一个简单的配方，将 PSI 协议的一个特别常见的形式变成一个具有 Cardinality 的隐私集合交集求和协议。

4.1 隐私集合求交集：概述

在一长串的工作中 [14]、[15]、[17]、[20]、[22]、[26]、[32]、[33]、[37]、[38]、[49]、[52]、[55]、[56] 已经广泛地研究了私有集相交。有几项工作将各方限制在只学习交集的 Cardinality [1], [13], [26], [33], [36], [44], [57]。

最近集合相交的专门协议中最普遍的技术，也是目前最有效的 PSI 构造的基础 [37], [48]，是基于不经意伪随机函数（OPRF）的概念 [25]。这种方法的高层次思想是用相应的 PRF 评估取代两个输入集中的项目，其中一方拥有 OPRF 密钥，可以在本地获得其伪随机评估，而 PRF 的不经意评估特性被用来使另一方获得其 PRF 值。现在两方中的任何一方都可以使用输入集的伪随机表示来计算交集，它也将拥有交集 PRF 值与原始输入集值的映射。不同的论文提出了不同的 OPRF 实例化方法，其中目前最有效的方法是使用随机不经意转移（ROT），这是对不经意转移 OT 扩展协议的修改 [52]，作为允许单一不经意评估的 OPRF。此外，集合相交协议被简化为许多更小的集合相交协议，其中一方总是有一个单元素的输入集合，这些可以使用基于 ROT 的 OPRF 的有限功能来实现。这是通过在其中一方利用布谷鸟散列 [18] 来实现的，布谷鸟散列将其项目分布在最多为一个大小的桶中，而在另一方使用所有布谷鸟散列函数对每个输入元素进行简单散列。这时，双方对发送到双方输入的每个桶的项目运行一个小型 PSI 协议。

另一种计算集合相交的方法，在 Dong 等人的工作中被引入，后来被 Rindal 等人 [55] 在恶意集合相交的背景下加强，利用布隆过滤器（BF）的概念 [4]。双方就布隆过滤器的哈希函数参数达成一致。第一方计算一个混乱的布隆过滤器，它的位置包含随机值，其约束条件是如果一个元素出现在集合中，那么布隆过滤器中对应于其散列位置的值是该元素的加法份额。第二方为其输入集构建一个具有二进制值的常规布隆过滤器。然后，双方运行不经意传输协议，第二方从第一方的混乱的布隆过滤器中检索元素，只检索其自身布隆过滤器中的值为 1 的位置。第二方现在可以检查它的哪个输入元素在它通过 OTs 获得的部分乱码 BF 所代表的交集中。

与我们部署的方法类似，也有基于决策性 Diffie-Hellman（DDH）计算假设的工作，它来自一些较早的工作 [14]、[33]、[34]、[38]、[56]。其总体思路如下。双方在一个 DDH 成立的组中哈希他们的值。每一方都有一个秘密的指数化密钥。双方使用他们的密钥对其散列的输入元素进行指数化，并交换结果。他们进一步对收到的每个集合中的元素进行指数化，并将结果发回。现在每一方都可以在本地计算交集。从技术上讲，这种方法可以被认为是 OPRF 方法的一个实例，其中 OPRF 密钥是共享的 [34]。

PSI 问题也被直接使用一般的两方计算技术来解决。使用混淆电路技术的作品允许计算交集的 Cardinality，以及交集关联值中项目的关联值的更一般的函数。Huang 等人的工作 [32] 利用 SortCompare-Shuffle 方法，该方法使用深度为 的电路来执行集合相交。Pinkas 等人的 Phasing 技术 [49] 将项目哈希到桶，并使用混淆电路来执行的二进制求交集。最近，几个部分并发的工作 [11]，[31]，[51] 结合现代 PSI 工具，如相位和排序洗牌比较混淆电路，以创建新的协议，允许各方输出交集中项目的共享。这允许双方对交集中项目的关联值进行任意的计算，包括学习关联值的总和。这些作品提供了非常有竞争力的计算效率，其代价是由于使用了需要比特加密和安全比较输入的技术（包括混淆电路）而增加了通信。然而，这些作品有一个强大的优势，即它们允许计算交点上的任意函数。

也有一些作品针对专门的设置来获得额外的效率。在不平衡输入集的设置中，Chen 等人 [10] 利用完全同态加密来创建 PSI 协议，该协议提供了更好的通信效率，同时允许检索交集中项目的相关数据。[35] 探索离线预计算，以最大化 PSI 的在线效率。一些作品也依赖于额外的一方或多个非共存的服务器，以计算总的统计数据，例如 [12]，[27]，[40]。

4.2 将 PSI 转化为 PIS：标签、洗牌和聚合

正如介绍中所讨论的，隐私集合交集求和问题可以被看作是隐私集合求交集功能的扩展，此外，PSI 功能是我们功能的一个隐含组成部分。因此，我们构造的自然起点是现有的 PSI 协议（我们部署的协议和我们的新构造都是如此）。我们从隐私集合求交集 (PSI) 到隐私集合交集求和 (PIS) 的高级秘诀如下：

  1. 我们的每个协议都采用了现有的 PSI 方法，并加入了一个洗牌步骤。这个想法首次出现在文献 [33] 中，其效果是将 PSI 协议变成了一个隐私交集 Cardinality 协议：洗牌让参与者计算有多少项目在交集中，但不知道具体有哪些项目。

  2. 与标识符一起，我们插入相关值的同态加密作为 "标签"。这些标签伴随着标识符通过 PSI 协议和洗牌步骤。当一方最终计算洗牌后的交集时，该方也可以同态地将所有 "标签" 加在一起，以计算相关值的加密交集，随后可以解密。

这个秘诀，我们称之为 "标签、洗牌、聚合"，在概念上是直截了当的，而且立即吸引人。然而，事实证明，对每个协议的详细应用会有很大的不同，对这个配方的天真应用会导致对协议通信和计算成本的重大影响。作为一个例子，我们的每一个协议都以不同的方式使用了一个底层的加法同态加密方案。事实证明，所选择的加法同态加密的具体选择对效率有巨大的影响，特别是像分档这样的功能的可用性。这些权衡将在附录 B 中详细讨论。事实上，我们认为对不同方法的仔细优化和比较是我们工作的一个关键贡献。

标签 - 洗牌 - 聚合方法的一个积极特征是，我们得到的每一个协议都自然而然地退化为计算交集大小的协议，只需跳过 "标签" 和 "聚合" 步骤。

考虑到这一秘诀，我们的方法是采取现有 PSI 方法所依据的最有前途的主要技术，并将其修改为隐私集合交集求和的设置，在效率方面比较所得到的协议。

随机 OT 集合相交技术是我们在第 4.3.1 节中描述的第一个新的隐私集合交集求和协议的基础，该协议使用同态加密和洗牌来隐藏确切的相交，同时对它进行聚合。

我们在第 4.3.2 节中介绍的第二个隐私集合交集求和的构造是受使用加密布隆过滤器的技术启发。

揭示交集的大小：应用上述配方的一个重要的副作用是，我们所有的协议除了揭示交集之和外，还揭示了交集的大小。在我们考虑的商业应用中，这实际上是一个理想的特征：各方实际上想了解有多少项目是共同的。然而，有可能在其他环境中，揭示交集的大小是不可取的泄漏。在这些情况下，这种额外的泄漏将是我们的配方和协议的一个缺点。

4.3 具有 Cardinality 的隐私集合交集求和的新协议

在这一节中，我们介绍了我们的新加密协议，用于具有 Cardinality 的隐私集合交集求和，它利用了最近的随机 OT 和布隆过滤器技术，用于集合相交。

4.3.1 基于随机 OT 的协议

在这一节中，我们描述了一个基于随机 OT 的相交和协议，它被用于现有的 PSI 解决方案中 [20], [49], [52], [55]。我们认为这是第一个从随机 OT 中构建的具有 Cardinality 的隐私集合交集求和功能。请注意，我们的构造可以自然地修改为隐私计算 PSI-cardinality 的协议。

我们使用 A 节中定义的下列原语：

  • 具有以下功能的随机 OT。 没有输入，获得一个可以在某个已知域上进行评估的 PRF 密钥 。 有输入 ，并收到 ，即 PRF 在 点上的评估值。此外， 在输入的多项式子集（包括或不包括 ）上的任何评估对 来说都是伪随机的。
  • 一个加法同态加密方案（ , , ）。

我们在图 3 中展示了我们的协议 。在高层次上， 协议类似于 [37] 的基于 Batched-OPRF 的 PSI。然而，由于我们还希望交集被隐藏，我们引入了另一个步骤，即对分批 OPRF 的输出进行洗牌和重新掩码。这种洗牌是由 OPRF 接收者对成批的 OPRF 输出进行加密，并将加密结果发送给 OPRF 发送者来执行。然后，发送者以同态方式在每个密文中添加一个随机值 ，并在发送回之前在彼此之间洗牌密文。这隐含地将 OPRF 输出 改为 ，这也是伪随机的，可以被看作是一个 "新的"OPRF。当接收者解密时，它因此学习了在其每个输入上评估的 "新"OPRF，但以洗牌的顺序。一旦我们有了这种类型的洗牌 OPRF，就可以很自然地建立一个关于相交和和交集 Cardinality 的协议。

我们注意到，[31] 和 [11] 与我们的协议有一些高层次的相似之处，因为他们采用了 [37] 风格的桶，并采用了额外的技术来隐藏交集中的具体项目。我们是通过洗牌来隐藏交集的，而 [31] 和 [11] 是通过对每个桶进行定制的 MPC 子协议来实现的。

假设布谷鸟散列失败的概率可以忽略不计，并且随机 OT 输出的碰撞概率可以忽略不计，那么该协议的正确性立即从检查中得出。

我们协议的安全性来自于加密方案的安全性和随机 OT 协议的安全属性。安全性是用一个标准的混合论证来证明的，其中加密被替换为零的加密，而随机 OT 的输出被替换为不相关的均匀随机值，这样一来，交集大小和交集总和保持不变。我们在此说明这些定理。这些定理证明，在真实执行中互动的诚实方的观点可以被一个只知道交集总和和交集大小的模拟器模拟出来。

定理 3（ 中针对 的 HBC 安全）：存在一个 模拟器 ，使得对于所有安全参数 和输入 ， ： 其中 是 的输入大小， 是相交集合， 是其 cardinality。

定理 4（ 中针对 的 HBC 安全）：存在一个 模拟器 ，使得对于所有安全参数 和输入 ， ： 其中 是 的输入大小， 是相交集合， 是相交集合的和。

正式的安全证明在附录 E。

图 3

图 3： ：基于随机 OT 的隐私集合交集求和协议

基于随机 OT 的隐私集合交集求和协议

  • 输入：

    • ：设置
    • ：设置元组

  • 设置阶段： 和 各自生成一个加法同构的加密密钥对 和 ，并交换公钥 和 。

  • 协议步骤：

    1. 和 选择布谷鸟哈希表大小为 ，储藏室大小为 ，以及 个哈希函数： 将输入映射到桶 。

    2. 将其项目使用布谷鸟散列函数 散列到 个桶和一个大小为 的储藏室中，其中每个桶最多包含一个项目。 用一个假的值来填补所有的空桶和储藏室中的空位。我们把 的项目（包括假的值和真实值）称为 ，其中项目 是储藏室中的项目。如果散列失败， 就会中止协议。

    3. 对于每个 部分，运行一个随机 OT，其中 获得一个 PRF 密钥 ， 获得评估值 。

    4. 将所有评估值用公钥 加密并发送至 ：

    5. 选择 个随机值 ，对于每个 ，计算： 。 将集合 打乱顺序后发送给 。

    6. 对于每个 ， 计算： 如果任何 的大小小于 ， 用假的随机元素填充 ，直到它的大小为 。 向 发送集合 ，其中组元的顺序被随机打乱，以隐藏每个 的哪些元素对应于哪个散列函数或存储索引。

    7. 对所有的 值进行解密，得到 ，与收到 发来的 计算交集，最后对编号为 的交集元素对应的 进行同态累加，得到加密的交集和。令 为解密值的集合， 计算： 将 重新随机化为 ，并将其发送给 。

  • 输出： 解密 以恢复 ，并输出 ，等于 ，即交集和。

4.3.2 基于布隆过滤器的协议

在本节中，我们描述了一个基于使用加密布隆过滤器的隐私集合交集求和协议，扩展了 PSI 方法 [17]、[20]、[22]。

我们使用附录 A 中定义的以下原语：布隆过滤器 ，加法同态加密方案（ ， ， ）。我们请读者参考附录 A，特别是定义 6，了解布隆过滤器的定义和符号。

我们在图 4 中展示了该协议。在高层次上，一方将其输入数据库插入布隆过滤器，并在其密钥 下使用加法同态加密方案对布隆过滤器的每个比特进行加密。然后，该方将加密后的布隆过滤器发送给另一方，后者以同态方式计算其元素在布隆过滤器中的成员资格。如果一个项目在布隆过滤器中，该方将同态计算一个零的加密，如果它不在布隆过滤器中，该方将计算一个统一的随机值的加密。它将这些 "成员" 密文按洗牌顺序发送给第一方，然后第一方可以解密以了解有多少项目在交集中。第二方也在自己的密钥 下发送同态加密的关联值与成员密文，允许第一方计算交集之和。第一方可以对最终的相交和进行加法掩码，然后解开第二方解密的值的掩码。

上述协议的正确性可以直接看到，除了在以下情况下：

  • 在布隆过滤器中存在碰撞，并且
  • 在步骤 4b 中， ，但 。

通过适当选择布隆过滤器的大小和哈希函数的数量，可以使布隆过滤器碰撞的概率可以忽略不计。 ，但 的概率可以通过使加密方案的消息空间呈指数级增长而变得可以忽略不计。

该协议的安全性来自于加法同态加密方案的安全特性，以及布隆过滤器中可忽略的碰撞概率。该证明使用一个标准的混合论证进行，它用 0 的加密替换了加密的关联值，同时保持相交和不变。

正式的安全证明出现在附录 F 中。它表明，每一方的观点都可以只使用交集大小和来模拟。

图 4

图 4： ：加密的基于布隆过滤器的隐私集合交集求和协议。

5 测量

在这一节中，我们介绍了第 4.3.1 节和第 4.3.2 节中介绍的我们的两个新的具有 cardinality 的隐私集合交集求和协议的实现的测量结果，以及第 3.1 节中描述的我们部署的协议的额外测量结果，包括部署的协议和使用不同同态加密方案的变体。我们还将具体的成本与之前报道的基于混淆电路的方案的数字进行比较，特别是作品 [31]、[49]、[50]、[52]，它们是在隐私交集上计算功能的最知名的作品。我们的比较包括基于 "批量计算" 场景的货币成本，使用表 1 中资源成本的 GCP 云定价。

在表 3 和表 4 中，我们以不同类型的操作和不同类型的传输元素的数量来表示每个协议的渐近成本。根据这些数字，我们预计 DDH 协议将有最好的通信，而在计算方面最有效的协议将取决于指数化和同态操作的相对成本，这一点我们通过实验来研究。

5.1 参数和加密方案

我们协议的所有计算成本测量都是以双方的总时钟运行时间为基础的，运行在一台具有英特尔至强 CPU E5-1650 v3（3.50 GHz）和 32GB 内存的台式工作站的单线程上，这与我们部署环境中的机器类似。计算成本不包括各方之间通过网络传输文件的时间。

对于所有的方案和数据库规模，我们假设输入域是 位字符串的集合，相关值最多为 位。我们还认为关联值的总和是以 位为界限的。所有的计算成本都是假设每一方的输入中的每个条目都在集合的交集中（在所有协议中，这使计算量最大化）。

现在我们描述一下每个协议的加密方案和参数的选择。

基于随机 OT 的协议：我们使用 Paillier 加密法对 值进行加密。我们用 768 位素数实现 Paillier 加密，因此每个密文为 3072 位，明文空间为 1536 位。对于随机不经意传输的变体，我们选择以下参数。

Cuckoo Hash：我们使用 Demmler 等人 [18] 的附录 B 中提供的启发式方法来选择 Cuckoo 散列参数。对于我们考虑的输入规模，这些启发式方法需要 个哈希函数，没有储藏室，布谷鸟哈希表可以容纳 个元素，有不大于 个桶。

随机 OT：我们使用 Kolesnikov 等人 [37] 的 Batched Random OT 协议，有 128 个基础公钥 OT 和伪随机码输出长度 448 位。对于实际的伪随机码，我们使用基于 SHA256 的 PRG，通过本地指令加速。我们还使用 SHA-256 作为 [37] 协议的哈希函数。

基于布隆过滤器的协议：我们使用指数 ElGamal 来加密布隆过滤器的比特。我们在一个具有 256 位组元的椭圆曲线上实现指数 ElGamal。如附录 B 所述，指数 ElGamal 很适合用于加密布隆过滤器，因为与 Paillier 或 Ring-WE 相比，它的密文相对较小。唯一的成本是解密，这需要计算离散对数，然而在基于布隆过滤器的协议中，我们只需要检查解密的值是否为 0，这可以非常有效地完成。我们还根据每一方持有的项目数量动态地选择哈希函数的数量和布隆过滤器的大小，基于所有项目的布隆过滤器错误碰撞的概率为 。也就是说，我们设置的参数，除了 的概率外，都能保证相交的正确性。

对于我们的 DDH 协议，我们使用 作为曲线，并使用 作为随机预言机，如第 3.2 节所述。

最后，为了加密相关值，我们使用 "槽式" 加密来展示测量结果，每个相关值都被加密到一个不同的槽中。我们使用具有 位密文模数和 位明文模数的 ，每个密文有 个系数，每个系数有 位误差。我们用 比特的随机性来掩盖和密文中的错误，这导致了至少 个统计学上的错误隐藏（即使我们最大的输入规模为 条）。每个密文是 ，可以容纳 个每个 位的值。更多细节见附录 B。我们通过实验发现，有槽的 加密与有槽的 优化的 加密的通信成本大致相同，而需要的计算量明显减少。我们在附录 H 中对不同的同态加密方案进行了额外的比较。

5.2 测量的讨论

我们在表 5 中介绍了我们的测量结果，并在表 6 中介绍了货币成本。我们显示了基于 DDH 的已部署协议以及基于 ROT 和 BF 的两个新协议的成本，使用 RLWE 作为相关值的同态加密方案，还比较了我们的已部署协议，它使用 DDH 协议和 Slotted Paillier 作为加密方案（见第 3.2 节）。

我们看到，货币成本密切跟踪通信成本。使用 Paillier 的 DDH 协议具有最简洁的通信，也是最有效的货币成本，而 ROT 协议的货币成本和通信成本都要高出 15 倍，而基于 BF 的协议则要高出 100 倍。DDH 协议，特别是用 RLWE 作为同态加密，被证明是我们计算效率最高的协议，比 ROT 和 BF 协议分别快 25 倍和 40 倍。最后，采用 RLWE 的 DDH 协议的货币成本比采用 Paillier 的 DDH 协议小 11%，计算量减少约 40%。

5.3 与混淆电路作品的比较

在本节中，我们将具体的成本（计算、通信和货币）与现有的基于混淆电路的工作中提出的成本进行比较，特别是 [31]、[49]、[50]、[52]。对于这些成本，我们在很大程度上依赖于 [50] 的出色阐述，大量借鉴了 [50] 的表 3 和表 5。

对于所有的 Garbled Circuit 协议，我们假设每一方的输入中的标识符被散列成 比特长，其中 n 是输入大小：这可以防止除概率 以外的散列碰撞。

表 7 中列出了通信、计算和货币成本的比较。

我们注意到，由于几个原因，这些比较是不完美的。其中重要的一点是，[50] 中提出的运行时间包括在局域网上的通信传输时间，而对于我们的协议，我们忽略了通信的时间，只包括计算的运行时间。这意味着我们在某种程度上高估了混淆电路式解决方案的计算成本。此外，测量使用的执行环境略有不同。另一点是，[50] 中的混淆电路式解决方案的通信成本只是针对 PSI 功能，而不是针对隐私集合交集求和。我们忽略了与计算相交和有关的额外成本，因此在某种程度上低估了 Garbled-Circuit 式解决方案的通信成本。

即使有这些注意事项，我们相信这个比较是有参考价值的，并且证明了我们的预期，即 Garbled Circuit 解决方案在计算上比我们提出的解决方案更快，但也产生了明显的通信成本。由于通信成本的巨大差异，在我们的成本模型中，这些协议的货币成本也要昂贵得多。

表 7 显示，基于 ROT 的协议和基于 DDH 的协议的两个变体，包括部署的协议，在货币方面比任何基于混淆电路的协议都要便宜。特别是，对于所考虑的数据大小，部署的协议比基于混淆电路的最便宜的协议 [50] 便宜 20-30 倍。我们基于布隆转换器的新协议也比除 [50] 之外的所有基于混淆电路的解决方案更便宜。

在本文新提出的协议中，就货币成本而言，基于 DH 的协议仍然是最便宜的。使用 Paillier 的 DH 协议（也就是我们部署的协议）在货币成本上比基于 RLWE 的变体要贵，但差别很小（大约 10%）。同时，基于 RLWE 的协议在计算上要便宜 40%。这意味着基于 RLWE 的协议在计算成本较高或通信成本比我们考虑的估值便宜的情况下可能特别有用。

表 3

表 3：每个协议中的计算操作。数字是双方的总和，每一方有 个输入。"指数" 是分组指数的数量（或 "公钥" 操作）。同态操作是指同态加密、解密和加法的数量。我们假设同态操作具有相同的成本。 指的是 个随机 OT 的计算成本。 是布谷鸟哈希 项的成本。 是将 个项目插入布隆过滤器的成本。

表 4

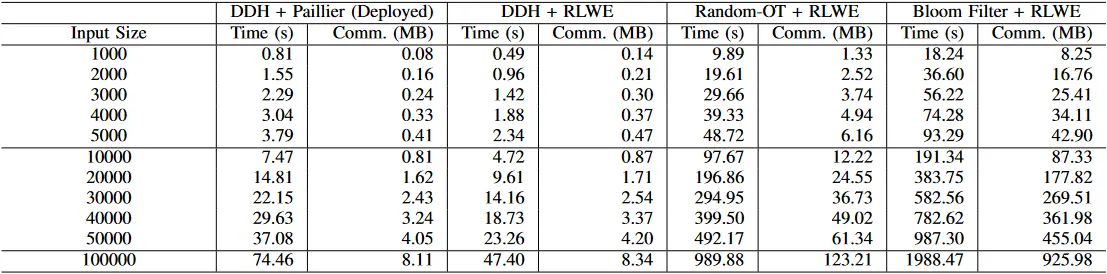
表 4：每个隐私集合交集求和协议中的通信。所列数字是双方的总和，每方有 个输入。组元素是指传输的 EC 曲线元素的数量。HE Ciphertexts 是指传输的同态加密的数量，不包括优化，如插槽。 指的是 个随机 OT 的通信成本。

表 5

表 5：隐私集合相交和协议的计算时间和网络成本的比较。我们包括已部署的协议（使用 Paillier 加密），以及使用有槽的 Ring-LWE 加密来加密相关值的变体。

表 6

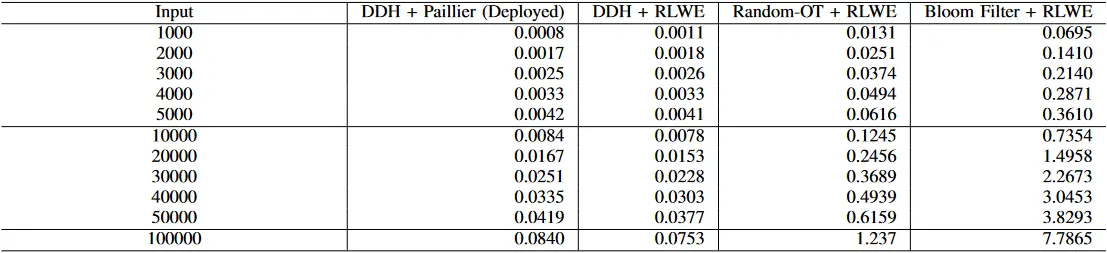
表 6：我们的 PIS 协议变体的货币成本比较（美分）。我们包括已部署的协议（使用 Paillier 加密），以及使用插槽式 Ring-LWE 加密来加密相关值的变体。资源评估使用表 1 中的 GCP 成本。

表 7

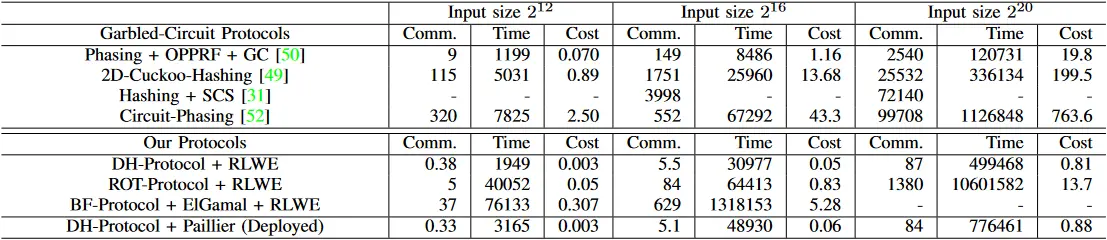
表 7：混淆电路协议和我们的解决方案之间的通信、计算和货币成本的比较。混淆电路协议的成本来自 [50] 的表 3 和表 5，仅是 PSI 的成本，不包括交叉和的成本。混淆电路协议还包括由于局域网上的网络通信时间，而我们的解决方案不包括网络通信时间。所有的通信费用以 MB 为单位，所有的时间以毫秒为单位，所有的 "成本" 是货币成本，以美分（USD）为单位，使用表 1 中 GCP 的资源估值。缺少的测量值要么是由于不可用的测量值，要么是由于计算耗尽了内存。

6 总结

我们描述了在一个行业环境中部署一个安全的计算协议，作为不同公司之间业务互动的解决方案。我们的工作所解决的问题是保护隐私的综合广告转换的归属。我们描述了我们认为使这个问题很适合安全计算解决方案的因素，并描述了我们设计上的各种实际限制。

我们所部署的协议之所以被选中，是因为它的简单性，同时也是因为它的通信效率，这对货币成本有很大的影响。我们还根据最近的进展，重新审视了私人有底线的相交和问题，在此基础上我们构建了两个新的协议。我们实现了所有的构建，以评估和比较它们的具体成本，包括货币成本。从我们的测量结果来看，除了一个协议外，所有协议在货币成本方面与安全计算交集上的通用函数的方法相比都很好。我们部署的协议被发现在货币成本方面比通用方法便宜 20 倍。我们的其他解决方案提供了更好的计算，以换取通信。

参考文献

  1. Agrawal, R., Evfimievski, A.V., Srikant, R.: Information sharing across private databases. In: SIGMOD Conference. pp. 86–97. ACM (2003)

  2. Araki, T., Furukawa, J., Lindell, Y., Nof, A., Ohara, K.: Highthroughput semi-honest secure three-party computation with an honest majority. In: ACM Conference on Computer and Communications Security. pp. 805–817. ACM (2016)

  3. Bellare, M., Rogaway, P.: Random oracles are practical: A paradigm for designing efficient protocols. In: ACM Conference on Computer and Communications Security. pp. 62–73. ACM (1993)

  4. 布隆，B.H.: Space/time trade-offs in hash coding with allowable errors. Communications of the ACM 13 (7), 422–426 (1970)

  5. Bogdanov, D., Talviste, R., Willemson, J.: Deploying secure multiparty computation for financial data analysis - (short paper). In: Financial Cryptography. Lecture Notes in Computer Science, vol. 7397, pp. 57–64. Springer (2012)

  6. Bogetoft, P., Christensen, D.L., Damg ̊ ard, I., Geisler, M., Jakobsen, T.P., Krøigaard, M., Nielsen, J.D., Nielsen, J.B., Nielsen, K., Pagter, J., Schwartzbach, M.I., Toft, T.: Secure multiparty computation goes live. In: Financial Cryptography. Lecture Notes in Computer Science, vol. 5628, pp. 325–343. Springer (2009)

  7. Bonawitz, K., Ivanov, V., Kreuter, B., Marcedone, A., McMahan, H.B., Patel, S., Ramage, D., Segal, A., Seth, K.: Practical secure aggregation for privacy-preserving machine learning. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. pp. 1175–1191. ACM (2017)

  8. Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (leveled) fully homomorphic encryption without bootstrapping. TOCT 6(3), 13:1–13:36 (2014)

  9. Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 43(2), 831871 (2014)

  10. Chen, H., Laine, K., Rindal, P.: Fast private set intersection from homomorphic encryption. In: ACM Conference on Computer and Communications Security. pp. 1243–1255. ACM (2017)

  11. Ciampi, M., Orlandi, C.: Com 桶 ing private set-intersection with secure two-party computation. In: International Conference on Security and Cryptography for Networks. pp. 464–482. Springer (2018)

  12. Corrigan-Gibbs, H., Boneh, D.: Prio: Private, robust, and scalable computation of aggregate statistics. In: 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17). pp. 259–282 (2017)

  13. Cristofaro, E.D., Gasti, P., Tsudik, G.: Fast and private computation of cardinality of set intersection and union. In: CANS. vol. 7712, pp. 218–231. Springer (2012)

  14. Cristofaro, E.D., Kim, J., Tsudik, G.: Linear-complexity private set intersection protocols secure in malicious model. In: ASIACRYPT. Lecture Notes in Computer Science, vol. 6477, pp. 213–231. Springer (2010)

  15. Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Efficient robust private set intersection. In: International Conference on Applied Cryptography and Network Security. pp. 125–142. Springer (2009)

  16. Damg ̊ ard, I., Jurik, M.: A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In: Public Key Cryptography. Lecture Notes in Computer Science, vol. 1992, pp. 119–136. Springer (2001)

  17. Debnath, S.K., Dutta, R.: Secure and efficient private set intersection cardinality using 布隆 filter. In: International Information Security Conference. pp. 209–226. Springer (2015)

  18. Demmler, D., Rindal, P., Rosulek, M., Trieu, N.: Pir-psi: scaling private contact discovery. Proceedings on Privacy Enhancing Technologies 2018(4), 159–178 (2018)

  19. Diffie, W., Hellman, M.: New directions in cryptography. IEEE transactions on Information Theory 22(6), 644–654 (1976)

  20. Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. pp. 789–800. ACM (2013)

  21. Dwork, C., McSherry, F., Nissim, K., Smith, A.: Calibrating noise to sensitivity in private data analysis. In: Theory of Cryptography (2006)

  22. Egert, R., Fischlin, M., Gens, D., Jacob, S., Senker, M., Tillmanns, J.: Privately computing set-union and set-intersection cardinality via 布隆 filters. In: Australasian Conference on Information Security and Privacy. pp. 413–430. Springer (2015)

  23. ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE transactions on information theory 31(4), 469–472 (1985)

  24. Fan, J., Vercauteren, F.: Somewhat practical fully homomorphic encryption. IACR Cryptology ePrint Archive 2012, 144 (2012)

  25. Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Theory of Cryptography Conference. pp. 303–324. Springer (2005)

  26. Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: International conference on the theory and applications of cryptographic techniques. pp. 1–19. Springer (2004)

  27. Froelicher, D., Egger, P., Sousa, J.S., Raisaro, J.L., Huang, Z., Mouchet, C., Ford, B., Hubaux, J.P.: Unlynx: a decentralized system for privacy-conscious data sharing. Proceedings on Privacy Enhancing Technologies 2017(4), 232–250 (2017)

  28. Furukawa, J., Lindell, Y., Nof, A., Weinstein, O.: High-throughput secure three-party computation for malicious adversaries and an honest majority (2017)

  29. Gentry, C., Halevi, S., Smart, N.P.: Fully homomorphic encryption with polylog overhead. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques. pp. 465482. Springer (2012)

  30. Hellman, M.E., Pohlig, S.C.: Exponentiation cryptographic apparatus and method (Jan 3 1984), uS Patent 4,424,414

  31. Hemenway Falk, B., Noble, D., Ostrovsky, R.: Private set intersection with linear communication from general assumptions. In: Proceedings of the 18th ACM Workshop on Privacy in the Electronic Society. pp. 14–25 (2019)

  32. Huang, Y., Evans, D., Katz, J.: Private set intersection: Are garbled circuits better than custom protocols? In: NDSS (2012)

  33. Huberman, B.A., Franklin, M., Hogg, T.: Enhancing privacy and trust in electronic communities. In: Proceedings of the 1st ACM conference on Electronic commerce. pp. 78–86. ACM (1999)

  34. Jarecki, S., Liu, X.: Fast secure computation of set intersection. In: SCN. Lecture Notes in Computer Science, vol. 6280, pp. 418–435. Springer (2010)

  35. Kiss, ́ A., Liu, J., Schneider, T., Asokan, N., Pinkas, B.: Private set intersection for unequal set sizes with mobile applications. Proceedings on Privacy Enhancing Technologies 2017(4), 177–197 (2017)

  36. Kissner, L., Song, D.: Privacy-preserving set operations. In: Proceedings of the 25th Annual International Conference on Advances in Cryptology. pp. 241–257. CRYPTO’05, Springer-Verlag, Berlin, Heidelberg (2005), http://dx.doi.org/10.1007/11535218 15

  37. Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious prf with applications to private set intersection. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. pp. 818–829. ACM (2016)

  38. Lambæk, M.: Breaking and fixing private set intersection protocols. Tech. rep., Cryptology ePrint Archive, Report 2016/665, 2016. http://eprint. iacr. org/2016/665 (2016)

  39. Lapets, A., Volgushev, N., Bestavros, A., Jansen, F., Varia, M.: Secure multi-party computation for analytics deployed as a lightweight web application. Tech. rep., Computer Science Department, Boston University (2016)

  40. Le, P.H., Ranellucci, S., Gordon, S.D.: Two-party private set intersection with an untrusted third party. In: Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. pp. 2403–2420. ACM (2019)

  41. Meadows, C.: A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In: Security and Privacy, 1986 IEEE Symposium on. pp. 134–134. IEEE (1986)

  42. Mitzenmacher, M., Upfal, E.: Probability and computing: Randomized algorithms and probabilistic analysis. Cambridge university press (2005)

  43. Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)

  44. Narayanan, G.S., Aishwarya, T., Agrawal, A., Patra, A., Choudhary, A., Rangan, C.P.: Multi party distributed private matching, set disjointness and cardinality of set intersection with information theoretic security. In: International Conference on Cryptology and Network Security. pp. 21–40. Springer (2009)

  45. Pagh, R., Rodler, F.F.: Cuckoo hashing. J. Algorithms 51(2), 122144 (2004)

  46. Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: International Conference on the Theory and Applications of Cryptographic Techniques. pp. 223–238. Springer (1999)

  47. Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: SpOT-light: Lightweight private set intersection from sparse OT extension. In: CRYPTO (3). Lecture Notes in Computer Science, vol. 11694, pp. 401–431. Springer (2019)

  48. Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: Spot-light: Lightweight private set intersection from sparse ot extension. In: Annual International Cryptology Conference. pp. 401–431. Springer (2019)

  49. Pinkas, B., Schneider, T., Segev, G., Zohner, M.: Phasing: private set intersection using permutation-based hashing. In: Proceedings of the 24th USENIX Conference on Security Symposium. pp. 515530. USENIX Association (2015)

  50. Pinkas, B., Schneider, T., Tkachenko, O., Yanai, A.: Efficient circuit-based PSI with linear communication. In: EUROCRYPT (3). Lecture Notes in Computer Science, vol. 11478, pp. 122–153. Springer (2019)

  51. Pinkas, B., Schneider, T., Weinert, C., Wieder, U.: Efficient circuitbased psi via cuckoo hashing. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques. pp. 125–157. Springer (2018)

  52. Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on ot extension. In: Usenix Security. vol. 14, pp. 797–812 (2014)

  53. Pinkas, B., Schneider, T., Zohner, M.: Scalable private set intersection based on OT extension. ACM Trans. Priv. Secur. 21(2), 7:1–7:35 (2018)

  54. Rajan, A., Qin, L., Archer, D.W., Boneh, D., Lepoint, T., Varia, M.: Callisto: A cryptographic approach to detecting serial perpetrators of sexual misconduct. In: COMPASS. pp. 49:1–49:4. ACM (2018)

  55. Rindal, P., Rosulek, M.: Improved private set intersection against malicious adversaries. Tech. rep. (2016)

  56. Segal, A., Ford, B., Feigenbaum, J.: Catching bandits and only bandits: Privacy-preserving intersection warrants for lawful surveillance. In: FOCI (2014)

  57. Vaidya, J., Clifton, C.: Secure set intersection cardinality with application to association rule mining. Journal of Computer Security 13(4), 593–622 (2005)

  58. Yao, A.C.C.: How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science (sfcs 1986). pp. 162–167. IEEE (1986)

附录 A 前言、密码学原理和难度假设

A.1 符号

代表整数，而 代表非负整数。符号 表示集合 的 。符号 代表整数集合 中 ，，而 代表集合 。 设 是两方 和 之间的随机互动协议， 持有输入 ， 持有输入 。对于安全参数 ，我们使用符号 来表示 的协议中 的观点所对应的随机变量。一方的观点是该方的输入、其随机性以及该方在执行 期间收到的所有消息，包括另一方的中止。随机变量在 和 的随机性上变化。

A.2 决策性 Diffie-Hellman

定义 1（决策型 Diffie-Hellman [19]）。令 为一个以安全参数 为参数的群族。对于每一个在时间为 的多项式中运行的概率对抗者 ，我们定义 的优势为： 其中，概率是对 中的随机选择 、 的随机生成器 、随机 、 、 以及 的随机性。我们说，如果对于每一个这样的 ，存在一个可以忽略不计的函数，使得 的优势被 Cannot read property '4' of nullMath input error 所约束，则决定性的 Diffie-Hellman 假设对 成立。

换句话说，分布 和 在计算上是不可区分的。通过本文，我们将使用乘法概念来写群操作。

A.3 随机预言机模型

定义 2（随机预言机 [3]）。随机预言机 是一个从 到 的映射，通过均匀独立地选择 的每一个比特，对于每一个 ， 意味着一个无限长的输出，它可以被截断为任何固定的适当大小，取决于设置。

如果我们能够证明，当协议中对 的每一次调用都被对相同输入的随机预言机 的调用所取代时，我们就说该协议在将哈希函数 建模为随机预言机时是安全的。

A.4 加法同态加密方案

定义 3（加性同态加密）。一个加法同态加密方案由以下概率性多项式时间算法组成：

  • ：给定一个安全参数 ， 返回输出一个公私密钥对 ，并指定一个消息空间 。

  • ：给定公钥 和明文信息 ，可以计算出一个密文 ，即 下 的加密。

  • ：给定秘密密钥 和密文 ，人们可以运行 来恢复明文 。

  • ：给定公钥 和一组加密信息 的密文 ，可以同态计算出一个加密基础信息之和的密文，为便于说明，我们将其表示为为：

请注意，明文标量的同态乘法可以通过重复的同态加法来实现，这一点很简单。我们考虑的所有同态加密方案也都支持与明文标量的同态乘法。此外，我们将利用一个属性，即人们可以使用一个随机化的程序来随机化密文，表示为 。特别是，我们将利用 和 的分布在统计学上是接近的这一事实，即使面对持有秘钥 的对手。在流行的方案中，如 Paillier [46] 和 Exponential ElGamal [23]，这种 可以通过加一个额外的刷新加密 来实现。在基于 RLWE 的同态加密方案 [8] 中，这可以通过增加一个足够大的随机值来实现，以便淹没密文的 "噪音"。我们依靠加密的 CPA 安全的标准概念，意思是，非正式地，在不知道私钥 的情况下，不同信息的加密在计算上是不可区分的。

A.5 不经意伪随机函数（OPRF）

定义 4（不经意伪随机函数 [25]，[43]）。如果存在一些伪随机函数族 ，从而使 安全地计算出以下功能，则称一个两方协议 为不经意伪随机函数 (OPRF):

  • 输入：第一方持有一个评估点 ；第二方持有一个密钥 。
  • 输出：第一方输出 ；第二方不输出任何东西。

换句话说，OPRF 协议允许第一方使用第二方持有的密钥 接收输入 上的 的输出，同时向第二方隐藏输入 。此外，在第一方看来，对所有其他输入的 的评估仍然是伪随机的。

A.6 随机不经意传输 (ROT)

定义 5（随机不经意传输 [37]）。设 是一个伪随机函数族。如果一个两方协议 能安全地计算出以下功能，则称其为随机不经意传输协议 (ROT)：

  • 输入：第一方持有 个评估点 ；第二方没有输入。
  • 输出：第一方输出 ；第二方输出 个 。

也就是说，ROT 可以被看作是同时执行的多个 OPRF 协议，其中底层 PRF 的密钥是在 ROT 执行过程中动态生成的。就像在 OPRF 评估中一样，在第一方看来，任何 在任何点 上的输出仍然是伪随机的。（在 [37] 的执行中，技术上 PRF 族是一个具有相关密钥的 "松弛的"PRF 族。我们请读者参考 [37] 的细节，在此省略，因为这种区别对我们的协议或证明没有重大影响）。

A.7 布隆过滤器

定义 6（布隆过滤器 [4]）。布隆过滤器是一种概率数据结构，支持插入和成员检查。一个布隆过滤器的参数是由一个大小为 和一串随机选择的哈希函数 。一个空的布隆过滤器 由 个比特组成，每个比特都设置为 。在布隆过滤器中插入一个项目 是通过将布隆过滤器的第 位设置为 来实现的，检查一个项目 是否在布隆过滤器中是通过检查布隆过滤器的第 位对所有 都是 来实现的。

布隆过滤器有可能在成员资格测试中出现假阳性。一个元素 产生假阳性成员测试的概率取决于 、 和插入到布隆过滤器中的项目数量。[42] 是关于设置布隆过滤器参数的一个很好的参考。

A.8 布谷鸟哈希

定义 7（布谷鸟哈希 [45]）。布谷鸟哈希表是一个支持插入和成员测试的数据结构。它的参数有桶的数量 ，储藏室的大小 ，以及随机选择的 个哈希函数。一个空的布谷鸟哈希表有 个空桶。当把一个项目 插入表中时，如果任何一个桶 是空的，那么 就被放在这些桶中的一个。否则， 中的一个桶将被随机选择，该桶中的项目将被替换为 ，然后被驱逐的项目将被递归插入。如果这个过程在一组固定的迭代后没有结束，那么最后被驱逐的元素就会被放在一个特殊的桶中，称为储藏室。如果储藏室已经包含了 个项目，则插入算法失败。

为了检查一个项目 是否在布谷鸟哈希表中，我们要检查 中的每一个桶的项目。

[18] 通过大量的实验表明，当向 ， ， 和 的布谷鸟散列中插入 个项目时，布谷鸟散列失败概率小到 。

附录 B 同态加密方案的实例化

我们提出的三个隐私集合交集求和协议中的每一个都需要一个加法同态加密方案，以便对相关的值进行加密并对它们进行同态求和。基于随机 OT 的协议和基于布隆过滤器的协议还依赖于一个加法同态加密方案，以便对标识符本身进行加密和相交。同态加密方案的选择对每个协议的通信和计算成本都有很大影响。在本节中，我们讨论了我们可以使用的三种可能的加法同态加密方案，即 Paillier 加密 [46]、指数 ElGamal 加密 [23] 和基于 Ring-WE 的方案 [8]、[9]、[24]、[29]。我们讨论了每种方案的各种特点，以及可以应用于每种方案的优化。这些差异在图 5 中进行了总结。

B.1 Paillier 加密

加密 [46] 是一个著名的加法同态加密方案，其安全性基于决定性的复合剩余性假设。

它需要相对昂贵的模块化指数化（"公钥"）操作，以便加密和解密。 密文也有很大的明文和密文空间，当被加密的值很小时，这导致了很大的通信扩展。例如，使用典型的安全参数，一个 密文将有 位的密文空间和 位明文空间。然而，如果要加密和求和的相关值在 位的范围内，那么与明文相比，使用 会导致大约 倍的密文扩展。

然而， 方案的大明文空间可以通过移位加法将多个值打包成 "槽"，以创建一个大的地方，更好地利用大容量。较低的槽位也可以通过同态地乘以 的幂来移到较高的位置。

分槽有助于使 加密对关联值的加密更加高效：client 可以将不同的关联值 加密到每个槽中。一旦 server 确定哪些槽需要相加，它可以将这些值旋转到一个特殊的槽（即最高的槽），并同态地将经过旋转的密文相加，以计算出加密的总和。然后，server 可以用随机值掩盖其他槽，以隐藏这些槽中的任何剩余和，并将最终的密文送回给 client 解密。

槽需要足够大以容纳相关的值，并有一些额外的位以允许求和而不溢出，还有一些位以允许随机掩码。此外，只有一半的明文空间可以用于槽，以便将最低的槽旋转到最高槽的位置，而不会溢出明文空间。插槽也可以与 优化相结合 [16]，它允许增加 方案的明文空间，而密文大小的增加比例较小。

作为一个例子，考虑每个 位的关联值，在交叉和中有 个值（需要 位），并且每个槽有 个额外的位用于随机屏蔽。这导致每槽 比特。也考虑使用 优化， ，这意味着每个密文有 位的明文空间，而密文有 位的大小。每个密文最多可以容纳 个槽，并有掩码和旋转的空隙。因此，每个密文对其可容纳的相关值的大小的扩展是 ，这相当于 倍的扩展，比最初考虑的 倍有明显的改进。

B.2 指数级 ElGamal

指数 ElGamal 加密 [23] 也有公钥操作进行加密，但比 Paillier 加密的密文相对较小。椭圆曲线上的 ElGamal 的密文长度为 512 比特，对于一个 20 比特的明文值来说，它的扩展量为 25 倍。指数 ElGamal 的一个缺点是，解密是昂贵的，涉及解决明文空间的 DDH。这就限制了可以解密的明文的大小，大约为 60 比特，同时也阻碍了像槽的优化。

然而，如果要加密的值很小（例如 20 比特），而且要加在一起的数量也很小（例如 个元素，那么求和后的明文大小将是 36 比特，小到可以解密。这使得指数式 ElGamal 成为（无槽）Paillier 加密关联值的良好替代方案。通过使用内存中的查找表，也可以使解密更快。

在基于布隆过滤器的协议中，指数 ElGamal 是对 Paillier 的改进（第 4.3.2 节），我们使用加法同态加密来加密布隆过滤器的每一个比特，只需要测试解密的值是零还是非零。对于该协议，我们得到了更小的密文，而且没有计算效率的损失，因为测试一个密文是否解密为 在指数 ElGamal 方案中是非常便宜的。

B.3 基于环容错学习问题的密码系统

另一个选择是基于格的加密。这种类型的最有效的方案是基于 Ring-Learning-With-Errors 的难度 [8], [9], [24], [29]。与 Paillier 和指数级 ElGamal 等方案相比，基于 Ring-LWE 的加密方案通常也有相当的计算效率，因为它们在加密和解密时不涉及昂贵的模块化指数运算，而且其多项式运算可以使用数论变换（NTT）来加速。

基于 RLWE 的方案也有具有大的明文空间的密文，但这些自然分解为多个 "槽"，其中每个槽都是单独的加法同态。此外，槽可以通过将密文与对应于 x 的单次幂的明文单项式相乘而有效地同态旋转。因此，持有相关值的一方可以将一个相关值放入明文的每个槽中，并加密和发送密文给另一方，后者可以同态旋转密文，使要添加的值最终都在一个特别指定的槽中（例如，对应于多项式常数项的槽），然后同态添加旋转的密文，最后，用随机值屏蔽其他槽。

基于 RLWE 的加密方案的一个微妙之处在于用于随机化密文的 程序。事实上，所产生的密文的错误必须被掩盖，以隐藏用于创建它们的操作序列。为了做到这一点， 程序在统计上用大量的新噪音淹没了错误，以便在统计上隐藏哪些输入密文被使用。这引起了一些额外的通信开销。

附录 C 基于混淆电路式方法的分析比较

……

附录 D 基于 DDH 协议的安全分析

在本节中，我们将证明基于 DDH 的协议 的安全性，如图 2，第 3.1 节所示。该证明是在诚实但好奇的模型中，我们假设参与者诚实地遵循协议的步骤，但事后试图从协议记录中提取尽可能多的信息。这个模型仍然需要双方之间有一定程度的信任，不要偏离规定的协议。

我们证明了诚实但好奇的模型中的安全性；我们的证明与 Agrawal 等人 [1] 给出的证明相似。我们通过给出一个模拟器来证明安全性，该模拟器可以无差别地模拟协议中每个诚实的一方的观点，只给出该方的输入、交集的 cardinality 和交集的和（但不包括另一方的输入）。直观地讲，这将表明，每一方通过参与协议，除了交集的 cardinality 和交集的和之外，没有学到更多东西。

在这样的协议执行中，一方的视图由其内部状态（包括其输入和随机性）和该方从另一方收到的所有消息组成（该方发送的消息不需要成为视图的一部分，因为它们可以通过其视图的其他元素来确定）。

让 是一个随机变量，代表 在实际协议执行中的观点，其中随机变量的范围是所有各方的内部随机性，以及设置阶段的随机性（包括随机神谕）。

我们的第一条定理，我们从第 3.1 节重述，表明在协议 中 的观点可以被模拟，只需给定 的输入和交集的大小（而不是 的输入）。

定理 1（基于 的协议中针对 的诚实但好奇的安全性）。存在一个 PPT 模拟器 ，这样对于所有安全参数 和输入 ， 其中，表示的输入大小， 表示交集集合，表示交集集合的基数。

证明。我们在算法 1 中描述了模拟器算法。请注意，在第 2 轮中，与实际协议执行的主要区别在于，不是像实际执行一样发送和，而是使用具有相同大小交集的随机群元素和，以及加同态加密的 0。

我们认为 使用多步混合论证，其中相邻的每一对混合分布在计算上无法区分。

：协议实际执行中的视图。

：与相同，除了在第 2 轮中，发送的所有加性同态密文都被新的 0 加性同态加密替换。

：与相同，除了在第 2 轮的第 2 步中，Party 2 的消息中的被替换为，其中是中按字典顺序排列的最小元素，是中的随机元素。

：与相同。

：与相同，除了在第 2 轮的第 4 步中，Party 2 的消息中的被替换为，其中是中按字典顺序排列的最小元素，是中的随机元素。

与 相同。

，其中 : 与 相同，除了：

  • 在第二轮中发送的消息中， 被替换为 ，并且
  • 在第四轮中发送的消息中， 被替换为 ，

​ 其中 是集合 中尚未替换的字典序最小的元素， 是 中的随机元素。

： 在 输出的视图。

我们现在将证明上述序列中每个相邻的混合模型都是不可区分的。

我们首先观察到由于加法同态加密方案的 CPA 安全性质， 和 是不可区分的。我们还观察到混合模型对 和 是相同的。

现在我们需要证明形如 和 的混合模型是不可区分的。我们将根据混合模型的困难程度论证所有 的 和 是不可区分的。我们注意到形如 和 的混合模型也可以通过非常类似的论证证明不可区分。

考虑下面的算法 2，它以 DDH 元组和混合指数作为输入，并模拟：

我们观察到，算法 2 在输入和 DDH 元组时产生的输出分布与相同。要看到这一点，我们首先观察到随机预言机即使在重新编程之后也具有均匀随机的输出，因为所有重新编程的值都是一个生成元的随机幂次。接下来，将隐藏的指数解释为的密钥，所有在第 2 轮中由发送的模拟消息都具有的正确形式：在第 2 轮步骤 2 中未替换的消息具有形式，而在第 2 轮步骤 4 中发送的消息具有形式，AEnc。

现在我们将输入给的 DDH 元组替换为具有形式的元组。唯一的影响是，我们不再有，而是有。根据我们之前对解释的方式，这意味着。这个变化正是和之间的差异。因此，在输入和时的输出与完全相同。

通过上述论证，我们可以推断出如果任何攻击者可以区分 和 ，那么它就可以区分 和 。因此，根据假设的 难度， 和 是不可区分的。

我们第二个定理，重新陈述自第 3.1 节，证明了在基于 DDH 的协议中， 的视图可以仅通过的输入和交集求和 (而非的输入) 来模拟。

定理 2 (针对协议中的诚实但好奇安全性): 存在一个 PPT 模拟器，使得对于所有安全参数和输入， 其中 是 输入的大小， 是交集集合，而 是交集和。

证明：我们定义诚实地执行设置阶段，并诚实地执行对应于的操作。模拟发送的消息如下：

  • 在第 1 轮中，不发送的消息，而是发送个随机选择的元素。

  • 在第 3 轮中，不执行交集计算并计算交集总和，而是发送一个新的加性同态密文，该密文加密了其输入的值。

我们注意到，的输出与真实执行中的视图之间的唯一区别在于第 1 轮的消息。然而，通过使用简单的混合论证，可以证明输出的第 1 轮消息与真实执行中的消息不可区分：定义个混合形式，其中在每个连续混合中，将一个额外的 “真实” 第 1 轮消息形式替换为的随机元素。然后，可以基于是保密的且在中是困难的事实来证明相邻的混合对之间不可区分。细节与定理 1 的证明非常相似，我们将其作为练习留给读者。

附录 E 基于随机 OT 的协议的安全分析

在这个部分，我们证明了基于随机 OT 的私有交集求和协议在诚实但好奇的模型下的安全性，该协议在第 4.3.1 节和图 3 中介绍。

设为一个随机变量，代表着随机 OT 协议的实际执行中的视图，其中随机变量涵盖了所有参与方的内部随机性。

我们重述第 4.3.1 节中的定理：

定理 3（针对的诚实但好奇安全性，基于随机 OT 的协议）。存在一个 PPT 模拟器，对于所有安全参数和输入， 其中，是输入的大小， 是交集集合，是其基数。

证明：我们在算法 3 中描述了模拟器算法。

我们使用多步混合论证来证明：

每个相邻混合分布都是计算不可区分的。

：协议的真实执行中，的视图对应的传输记录。

：与相同，但在第 6 步中，将加同态密文替换为在下的 0 的新加密。

：与相同，但对于所有的，在第 6 步中，将中的元素替换为均匀随机值。

：与相同，但在第 5 步中，每个被替换为一个均匀随机值的加密，并且在第 6 步中，的相应元素（即中的元素）也被替换为。

：由输出的的视图。

我们现在论证上述序列中每个相邻的混合方案是无法区分的。首先注意到，由于加法同态加密方案的隐藏特性，和是无法区分的。和仅在于对于未持有的，值被替换为均匀随机值。因此，可以基于随机 OT 协议中未检索到的项目的伪随机性证明和是无法区分的。可以使用一次性密码加上随机值的特殊属性，以及定义 3 中讨论的同态加密方案的特殊属性，即新的加密与使用同态操作生成的加密是无法区分的，来证明和是无法区分的。最后，和是完全相同的分布。

由于每对相邻混合方案是无法区分的，因此我们得出结论： 我们现在论证在 ROT 协议 中， 除了交集和之外，从协议中学不到任何东西。我们重申第 4.3.1 节中的定理：

定理 4（对于 ROT 协议中的 Party 2 的诚实但好奇安全性）。存在 PPT 模拟器，使得对于所有安全参数和输入， 其中 是 的输入的大小， 是交集，而 是交集和。

证明：我们观察协议中的视图由以下内容组成：

  1. 是否由于布谷鸟哈希失败而中止（步骤 2）。

  2. 随机 OT 执行中发送方的视图（步骤 3）。

  3. 密文集合，这些密文是使用的密钥加密的（步骤 4）。

  4. 密文 CT，使用的密钥加密了交集和（步骤 7）。

观察到对于第 2 和第 3 个条目（随机 OT 协议中的发送方视图和使用另一个方的密钥加密的条目），什么也不知道。此外，对于第 4 个条目，看到一个加密了同态计算的交集和的密文。根据同态加密方案的特殊属性（参见定义 3），这与加密的新加密不可区分。最后，卡瓦雀哈希失败的概率可以通过适当选择参数使得可以忽略不计。

因此，我们可以模拟的视图如下：

  • 模拟器在步骤 2 中永远不会中止。

  • 在步骤 3 中，模拟器请求任意选择的值，以用于随机 OT 协议。

  • 在步骤 4 中，模拟器发送，以作为 0 的新加密。

  • 在步骤 7 中，模拟器发送 CT，以作为在下的新加密。

很容易证明，在上述模拟执行中，的视图与实际执行中的的视图是不可区分的。我们将详细的混合证明作为练习留给读者。

附录 F 基于布隆过滤器的协议的安全分析

……

附录 G "反向" 变体

……

G.1 基于 DDH 的 "反向" 协议

……

G.2 安全分析

……

附录 H 额外的测量

H.1 使用一个理想化的同态加密方案

……

H.2 为基于随机 OT 的协议使用不同的加法加密方案

……